(本小题满分15分)
已知二次函数 满足条件:
满足条件:
①当 时,
时, ,且
,且 ;
;
②当 时,
时, ;
;
③ 在R上的最小值为0
在R上的最小值为0
(1)求 的解析式;
的解析式;
(2)求最大的m(m>1),使得存在 ,只要
,只要 ,就有
,就有 .
.
已知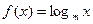 (m为常数,m>0且
(m为常数,m>0且 )
)
设 是首项为4,公差为2的等差数列.
是首项为4,公差为2的等差数列.
(1)求证:数列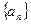 是等比数列;
是等比数列;
(2)若 ,且数列{bn}的前n项和
,且数列{bn}的前n项和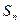 ,当
,当 时,求
时,求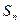
(3)若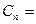
 ,问是否存在
,问是否存在 ,使得
,使得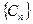 中每一项恒小于它后面的项?
中每一项恒小于它后面的项?
若存在,求出 的范围;若不存在,说明理由.
的范围;若不存在,说明理由.
某厂家拟在2010年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)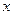 万件与促销费用
万件与促销费用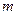 万元(
万元( )满足
)满足 (
( 为常数),如果不搞促销活动,则该产品的年销量只能是1万件。已知2010年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品的年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金)。
为常数),如果不搞促销活动,则该产品的年销量只能是1万件。已知2010年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品的年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金)。
(1)将2010年该产品的利润y万元表示为年促销费用m万元的函数;
(2)该厂家2010年的促销费用投入多少万元时,厂家的利润最大?
已知函数 (
( 为实数).
为实数).
(I)若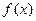 在
在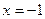 处有极值,求
处有极值,求 的值;
的值;
(II)若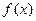 在
在 上是增函数,求
上是增函数,求 的取值范围.
的取值范围.
数列 的前
的前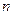 项和为
项和为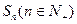 ,点
,点 在直线
在直线 .
.
⑴求数列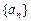 的通项公式;
的通项公式;
⑵ 数列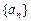 中是否存在三项,它们可以构成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由.
中是否存在三项,它们可以构成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由.
已知函数 图像的相邻两条对称轴之间的距离等于
图像的相邻两条对称轴之间的距离等于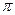 。
。
(1)求 的表达式;(要写出推导过程)
的表达式;(要写出推导过程)
(2)若 是直角三角形
是直角三角形 的内角,求
的内角,求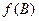 的值域。
的值域。