改革开放以来,我国高等教育事业有了突飞猛进的发展,有人记录了某村2001到2005年五年间每年考入大学的人数,为了方便计算,2001年编号为1,2002年编号为2,……,2005年编号为5,数据如下:
| 年份(x) |
1 |
2 |
3 |
4 |
5 |
| 人数(y) |
3 |
5 |
8 |
11 |
13 |
(1)从这5年中随机抽取两年,求考入大学的人数至少有 年多于10人的概率;
年多于10人的概率;
(2)根据这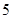 年的数据,利用最小二乘法求出
年的数据,利用最小二乘法求出 关于
关于 的回归方程
的回归方程 ,并计算第
,并计算第 年的估计值.
年的估计值.
参考:用最小二乘法求线性回归方程系数公式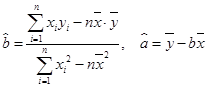
为了估计某产品寿命的分布,对产品进行追踪调查,记录如下:
| 寿命(h) |
100~200 |
200~300 |
300~400 |
400~500 |
500~600 |
| 个数 |
20 |
30 |
80 |
40 |
30 |
画出频率分布直方图;(2)估计产品在200~500以内的频率.
设函数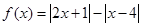
(1)解不等式 ;
;
(2)求函数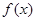 的最小值.
的最小值.
已知极坐标系的原点在直角坐标系的原点处,极轴为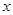 轴正半轴,直线
轴正半轴,直线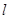 的参数方程为
的参数方程为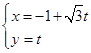 (
( 为参数),曲线
为参数),曲线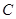 的极坐标方程为
的极坐标方程为 .
.
(1)写出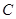 的直角坐标方程,并说明
的直角坐标方程,并说明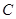 是什么曲线?
是什么曲线?
(2)设直线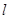 与曲线
与曲线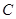 相交于
相交于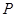 、
、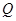 两点,求
两点,求 .
.
如图所示, 是⊙
是⊙ 直径,弦
直径,弦 的延长线交于
的延长线交于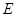 ,
,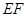 垂直于
垂直于 的延长线于
的延长线于 .求证:
.求证:
(1)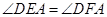 ;
;
(2) .
.
设函数 (
(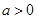 ).
).
(1)求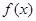 的单调区间;
的单调区间;
(2)求所有实数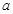 ,使
,使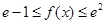 对
对 恒成立.
恒成立.
(注: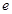 为自然对数的底数)
为自然对数的底数)