2013年我国多地出现雾霾天气，某企业抓住商机准备生产空气净化设备，该企业决定从以下两个投资方案中选择一个进行投资生产，方案一：生产甲产品，每件产品成本为a元（a为常数，且40＜a＜100），每件产品销售价为120元，每年最多可生产125万件；方案二：生产乙产品，每件产品成本价为80元，每件产品销售价为180元，每年可生产120万件，另外，年销售x万件乙产品时需上交0.5x2万元的特别关税，在不考虑其它因素的情况下：
（1）分别写出该企业两个投资方案的年利润y1（万元）、y2（万元）与相应生产件数x（万件）（x为正整数）之间的函数关系式，并指出自变量的取值范围；
（2）分别求出这两个投资方案的最大年利润；
（3）如果你是企业决策者，为了获得最大收益，你会选择哪个投资方案？
如图，把两个全等的Rt△AOB和Rt△COD分别置于平面直角坐标系中，使直角边OB、OD在x轴上．已知点A（1，2），过A、C两点的直线分别交x轴、y轴于点E、F．抛物线y=ax2+bx+c经过O、A、C三点．
（1）求该抛物线的函数解析式；
（2）点P为线段OC上一个动点，过点P作y轴的平行线交抛物线于点M，交x轴于点N，问是否存在这样的点P，使得四边形ABPM为等腰梯形？若存在，求出此时点P的坐标；若不存在，请说明理由．
（3）若△AOB沿AC方向平移（点A始终在线段AC上，且不与点C重合），△AOB在平移过程中与△COD重叠部分面积记为S．试探究S是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由．
如图，△ABC中，∠ACB=90°，D是边AB上一点，且∠A=2∠DCB．E是BC边上的一点，以EC为直径的⊙O经过点D．
（1）求证：AB是⊙O的切线；
（2）若CD的弦心距为1，BE=EO，求BD的长．
某饮料厂为了开发新产品，用
种果汁原料和
种果汁原料试制新型甲、乙两种饮料共50千克，设甲种饮料需配制
千克，两种饮料的成本总额为
元．
（1）已知甲种饮料成本每千克4元，乙种饮料成本每千克3元，请你写出与之间的函数关系式；
（2）若用19千克种果汁原料和17.2千克种果汁原料试制甲、乙两种新型饮料，右表是试验的相关数据；请你列出关于且满足题意的不等式组，求出它的解集，并由此分析如何配制这两种饮料，可使值最小，最小值是多少？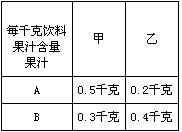
如图，已知A(-4，2)、B(n，-4)是一次函数
的图象与反比例函数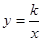
的图象的两个交点.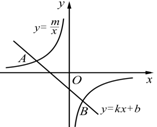
（1）求此反比例函数和一次函数的解析式；
（2）根据图象写出使一次函数的值小于反比例函数的值的x的取值范围；
（3）求△ABO的面积。
如图，把质地均匀的A、B两个转盘都分成三等分，玲玲和兰兰利用它们做游戏，同时自由转动两个转盘，当两个指针所停区域（停在分界线上重转）的数都是奇数或都是偶数时，则玲玲获胜，当两个指针所停区域的数是一奇一偶时，则兰兰获胜，列表或画树状图，用概率的知识说明这个游戏对她们是否公平？