阅读资料:

如图1,在平面之间坐标系xOy中,A,B两点的坐标分别为A(x1,y1),B(x2,y2),由勾股定理得AB2=|x2-x1|2+|y2-y1|2,所以A,B两点间的距离为AB= .
.
我们知道,圆可以看成到圆心距离等于半径的点的集合,如图2,在平面直角坐标系xoy中,A(x,y)为圆上任意一点,则A到原点的距离的平方为OA2=|x-0|2+|y-0|2,当⊙O的半径为r时,⊙O的方程可写为:x2+y2=r2.
问题拓展:如果圆心坐标为P(a,b),半径为r,那么⊙P的方程可以写为 .
综合应用:
如图3,⊙P与x轴相切于原点O,P点坐标为(0,6),A是⊙P上一点,连接OA,使tan∠POA= ,作PD⊥OA,垂足为D,延长PD交x轴于点B,连接AB.
,作PD⊥OA,垂足为D,延长PD交x轴于点B,连接AB.
①证明AB是⊙P的切点;
②是否存在到四点O,P,A,B距离都相等的点Q?若存在,求Q点坐标,并写出以Q为圆心,以OQ为半径的⊙O的方程;若不存在,说明理由.
某商店购进一批单价为16元的日用品,销售一段时间后,为了获取更多利润, 商店决定提高销售价格,经试验发现,若按每件20元的价格销售时,每月能卖360件; 若按每件25元的价格销售时,每月能卖210件.假定每月销售件数y(件)是价格x( 元/件)的一次函数.
(1)试求y与x之间的函数关系式;
(2)在商品不积压,且不考虑其他因素的条件下,问销售价格为多少时,才能使每月获得最大利润?每月的最大利润是多少?(总利润=总收入-总成本).
如图,射线 于点
于点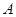 ,点
,点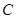 、
、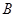 在
在 上,
上,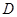 为线段
为线段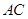 的中点,且
的中点,且 于
于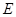 点.
点.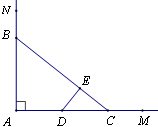
(1)若 ,△
,△ 的面积为
的面积为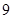 .
.
①直接写出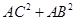 的值;
的值;
②求△ 的周长;
的周长;
(2)若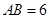 ,
,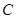 点在射线
点在射线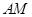 上移动,问此过程中,
上移动,问此过程中,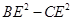 的值是否会为定值?若会,请求出这个定值;若不会,请求出它的取值范围.
的值是否会为定值?若会,请求出这个定值;若不会,请求出它的取值范围.
如图1所示,边长为a的大正方形中有一个边长为b的小正方形,如图2是由图1中阴影部分拼成的一个长方形。
(1)请问用这两个图可以验证公式法因式分解中的哪个公式?
(2)若图1中的阴影部分的面积是 ,
, ,求
,求 的值;
的值;
(3)试利用这个公式计算:
如图,在正方形网格中,有三个格点 ,且每个小正方形的边长为
,且每个小正方形的边长为 ,在
,在 延长线上有一格点
延长线上有一格点 ,连结
,连结 .
.
(1)如果 ,则△
,则△ 是________三角形(按边分类);
是________三角形(按边分类);
(2)当△ 是以
是以 为底的等腰三角形,求△
为底的等腰三角形,求△ 的周长.
的周长.
如图,在△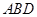 中,
中, ,
, ,
,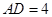 ,
,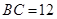 ,
,

(1)求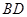 的长;
的长;
(2)求四边形 的面积.
的面积.