如图所示,倾角θ=30°的固定斜面上固定着挡板,轻弹簧下端与挡板相连,弹簧处于原长时上端位于D点。用一根不可伸长的轻绳通过轻质光滑定滑轮连接物体A和B,使滑轮左侧绳子始终与斜面平行,初始时A位于斜面的C点,C、D两点间的距离为L。现由静止同时释放A、B,物体A沿斜面向下运动,将弹簧压缩到最短的位置为E点,D、E两点间距离为 。若A、B的质量分别为4m和m,A与斜面之间的动摩擦因数
。若A、B的质量分别为4m和m,A与斜面之间的动摩擦因数 ,不计空气阻力,重力加速度为g,整个过程中,轻绳始终处于伸直状态,则( )
,不计空气阻力,重力加速度为g,整个过程中,轻绳始终处于伸直状态,则( )

A.A在从C至E的过程中,先做匀加速运动,后做匀减速运动
B.A在从C至D的过程中,加速度大小
C.弹簧的最大弹性势能为
D.弹簧的最大弹性势能为
(1)如图所示,某种自动洗衣机进水时,洗衣机缸内水位升高,与洗衣缸相连的细管中会封闭一定质量的空气,通过压力传感器感知管中的空气压力,从而控制进水量。当洗衣缸内水位缓慢升高时,设细管内空气温度不变,对于被封闭的空气,下列说法正确的是
A.分子间的引力和斥力都增大 B.分子的热运动加剧
C.分子的平均动能增大 D.体积变小,压强变大
(2)图中A、B气缸的长度和截面积均为30cm和2 0cm2,C是可在气缸内无摩擦滑动的、体积不计的活塞,D为阀门。整个装置均由导热良好的材料制成。起初,阀门关闭,A内有压强pA=2.0×105帕的氮气。B内有压强pB=1.0×105帕的氧气。阀门打开后,活塞C向右移动,最后达到平衡。假定氧气和氮气均为理想气体,连接气缸的管道体积可忽略。求:
0cm2,C是可在气缸内无摩擦滑动的、体积不计的活塞,D为阀门。整个装置均由导热良好的材料制成。起初,阀门关闭,A内有压强pA=2.0×105帕的氮气。B内有压强pB=1.0×105帕的氧气。阀门打开后,活塞C向右移动,最后达到平衡。假定氧气和氮气均为理想气体,连接气缸的管道体积可忽略。求:
(Ⅰ)活塞C移动的距离及平衡后B中气体的压强;
(Ⅱ)活塞C移动过程中A中气体是吸热还是放热(简要说明理由)
如图所示,在xoy平面内,O点即为坐标原点,x>0的区域存在垂直纸面向外的匀强磁场,磁感应强度为B=0.4T;x<0的区域存在沿x轴负 方向的匀强电场。现有一质量为m=6.0×10-9kg,带电荷量为q=3.0×10-7C的负粒子从x轴正方向上的M点以速度v0=20m/s进入磁场,v0与x轴正方向的夹角θ=45°,M点与O点相距为l=
方向的匀强电场。现有一质量为m=6.0×10-9kg,带电荷量为q=3.0×10-7C的负粒子从x轴正方向上的M点以速度v0=20m/s进入磁场,v0与x轴正方向的夹角θ=45°,M点与O点相距为l=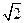 m。已知粒子再次通过x轴时速度方向恰好与x轴垂直。不计粒子重力。求:
m。已知粒子再次通过x轴时速度方向恰好与x轴垂直。不计粒子重力。求: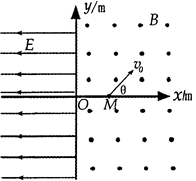
(1)粒子穿过y轴正半轴的位置以及穿过y轴正半轴时速度与y轴的夹角;
(2)x<0区域电场的场强;
(3)试问粒子能否经过坐标原点O?若不能,请说明原因;若能,请求出粒子从M点运动到O点所经历的时间
我市某路公共汽车的运行非常规则,先由静止开始匀加速启动,当速度达到v1=10m/s时再做匀速运动,进站前开始匀减速制动,在到达车站时刚好停住。公共汽车在每个车站停车时间均为△t=20s。然后以同样的方式运行至下一站。已知公共汽车在加速启动和减速制动时加速度大小都为a=1m/s 2,而所有相邻车站间的行程都为s=700m。有一次当公共汽车刚刚抵达一个车站时,一辆电动车刚好经过该车站一段时间t0=100s,已知该电动车速度大小恒为v2=6m/s,而且行进路线、方向与公共汽车完全相同,不考虑其他交通状况的影响,试求:
2,而所有相邻车站间的行程都为s=700m。有一次当公共汽车刚刚抵达一个车站时,一辆电动车刚好经过该车站一段时间t0=100s,已知该电动车速度大小恒为v2=6m/s,而且行进路线、方向与公共汽车完全相同,不考虑其他交通状况的影响,试求:
(1)公共汽车从车站出发至到达下一站所需的时间t是多少?
(2)若从下一站开始计数(即计数为第1站),公共汽车在刚到达第n站时,电动车也恰好同时到达此车站,则n为多少?
如图甲所示,一个质量m=0.1 kg的正方形金属框总电阻R=0.5 Ω,金属框放在表面绝缘且光滑的斜面顶端(金属框上边与AA′重合),自静止开始沿斜面下滑,下滑过程中穿过一段边界与斜面底边BB′平行、宽度为d的匀强磁场后滑至斜面底端(金属框下边与BB′重合),设金属框在下滑过程中的速度为v,与此对应的位移为s,那么v2—s图象(记录了线框运动全部过程)如图乙所示,已知匀强磁场方向垂直斜面向上。试问:(g取10m/s2)
(1)根据v2—s图象所提供的信息,计算出金属框从斜面顶端滑至底端所需的时间为多少?
(2)匀强磁场的磁感应强度多大?
(3)现用平行斜面沿斜面向上的恒力F作用在金属框上,使金属框从斜面底端BB′(金属框下边与BB′重合)由静止开始沿斜面向上运动,匀速通过磁场区域后到达斜面顶端(金属框上边与AA′重合)。试计算恒力F做功的最小值
如图所示,两个圆形光滑细管在竖直平面内交叠,组成“8”字形通道,在“8”字形通道底端B处连接一内径相同的粗糙水平直管AB。已知E处距地面的高度h=3.2m,一质量m=1kg的小球a从A点以速度v0=12m/s的速度向右进入直管道,到达B点后沿“8”字形轨道向上运动,到达D点时恰好与轨道无作用力,直接进入DE管(DE管光滑),并与原来静止于E处的质量为M=4kg的小球b发生正碰(ab均可视为质点)。已知碰撞后a球沿原路返回,速度大小为碰撞前速度大小的1/3,而b球从E点水平抛出,其水平射程s=0.8m,(g取10m/s2)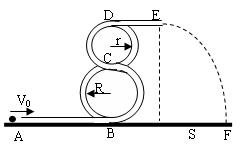
(1)求碰后b球的速度大小?
(2)求“8”字形管道上下两圆的半径r和R.?
(3)若小球a在管道AB中运动时所受阻力为定值,请判断a球返回到BA管道中时能否从A端穿出?