如图，已知四棱锥P—ABCD的底面为等腰梯形，AB∥CD，AC⊥BD，垂足为H，PH是四棱锥的高，E为AD的中点．
(1)证明：PE⊥BC；
(2)若∠APB＝∠ADB＝60°，求直线PA与平面PEH所成角的正弦值．
设函数f(x)＝sin xcos x－
cos(π＋x)cos x(x∈R)．
(1)求f(x)的最小正周期；
(2)若函数y＝f(x)的图象按b＝
平移后得到函数y＝g(x)的图象，求y＝g(x)在[0，
]上的最大值．
已知函数f(x)＝ln x－ax＋1在x＝2处的切线斜率为－
.
(1)求实数a的值及函数f(x)的单调区间；
(2)设g(x)＝
，对∀x1∈(0，＋∞)，∃x2∈(－∞，0)使得f(x1)≤g(x2)成立，求正实数k的取值范围；
(3)证明：
＋
＋…＋
<
(n∈N*，n≥2)．
已知二次函数f(x)＝ax2＋bx＋c (a≠0)且满足f(－1)＝0，对任意实数x，恒有f(x)－x≥0，并且当x∈(0,2)时，f(x)≤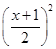
.
(1)求f(1)的值；
(2)证明：a>0，c>0；
(3)当x∈[－1,1]时，函数g(x)＝f(x)－mx (x∈R)是单调函数，求证：m≤0或m≥1.
如图，在四棱锥P—ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC＝90°，平面PAD⊥底面ABCD，Q为AD的中点，M是棱PC上的点，PA＝PD＝2，BC＝
AD＝1，CD＝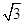
.
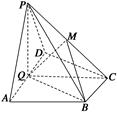
(1)若点M是棱PC的中点，求证：PA∥平面BMQ；
(2)若二面角M—BQ—C为30°，设PM＝tMC，试确定t的值．
：函数
为定义在
上的单调递减函数,实数
满足不等式
．命题
：当
时，方程
有解．求使“