(本小题满分10分)选修4-4:坐标系与参数方程
已知在直角坐标系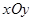 中,直线
中,直线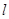 的参数方程为
的参数方程为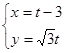 ,(
,(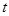 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,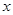 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线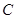 的极坐标方程为
的极坐标方程为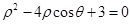
(Ⅰ)求直线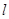 的普通方程和曲线
的普通方程和曲线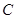 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设点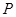 是曲线
是曲线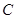 上的一个动点,求它到直线
上的一个动点,求它到直线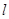 的距离
的距离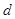 的取值范围.
的取值范围.
已知函数 ,且
,且
(1)求 ;
;
(2)判断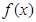 的奇偶性;
的奇偶性;
(3)判断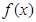 在
在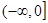 上的单调性,并证明。
上的单调性,并证明。
已知奇函数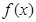 在
在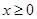 时的图象是如图所示的抛物线的一部分.
时的图象是如图所示的抛物线的一部分.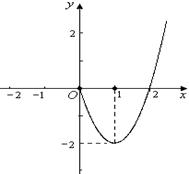
(1)请补全函数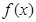 的图象;
的图象;
(2)写出函数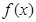 的表达式;
的表达式;
(3)写出函数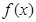 的单调区间.
的单调区间.
已知 ,
, ,若
,若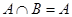 ,求
,求 的取值范围
的取值范围
已知函数f(x)= m·log2x + t的图象经过点A(4,1)、点B(16,3)及点C(Sn,n),其中Sn为数列{an}的前n项和,n∈N*.
(Ⅰ)求Sn和an;
(Ⅱ)设数列{bn}的前n项和为Tn , bn = f(an) – 1, 求不等式Tn£ bn的解集,n∈N*.
已知集合A= ,B=(2a,a2+1).
,B=(2a,a2+1).
(Ⅰ)当a=2时,求A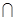 B;
B;
(Ⅱ)求使B 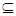 A的实数a的取值范围.
A的实数a的取值范围.