(15分)我国发射的“嫦娥一号”卫星发射后首先进入绕地球运行的“停泊轨道”，通过加速再进入椭圆“过渡轨道”，该轨道离地心最近距离为L1，最远距离为L2，卫星快要到达月球时，依靠火箭的反向助推器减速，被月球引力“俘获”后，成为环月球卫星，最终在离月心距离L3的“绕月轨道”上飞行，如图所示．已知地球半径为R，月球半径为r，地球表面重力加速度为g，月球表面的重力加速度为
，求：
(1)卫星在“停泊轨道”上运行的线速度大小；
(2)卫星在“绕月轨道”上运行的线速度大小；
(3)假定卫星在“绕月轨道”上运行的周期为T，卫星轨道平面与地月连心线共面，求在该一个周期内卫星发射的微波信号因月球遮挡而不能到达地球的时间(忽略月球绕地球转动对遮挡时间的影响)．
如图14所示，在坐标系xoy的第一象限内存在匀强磁场，磁场方向垂直于xoy面向里；第四象限内有沿y轴正方向的匀强电场，电场强度大小为E。一质量为m、带电荷量为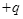
的粒子自y轴的P点沿x轴正方向射入第四象限，经x轴上的Q点进入第一象限。已知P点坐标为（0，-2），Q点坐标为（4，0），不计粒子重力。求：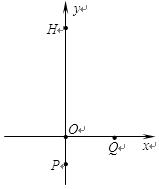
（1）求粒子过Q点时速度的大小。
（2）若磁感应强度的大小为一定值B，粒子将以垂直y轴的方向经H点进入第二象限，求B的大小及H点的坐标值；
（3）求粒子在第一象限内运动的时间t。
质量为m的小球A以速率v0向右运动时跟静止的小球B发生碰撞，碰后A球以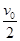
的速率反向弹回，而B球以
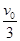的速率向右运动，求：
（1）小球B的质量mB是多大？
（2）碰撞过程中，小球B对小球A做功W是多大？
如图所示，质量为m的小物块（可视为质点）在粗糙水平桌面上做直线运动，经距离l后以速度υ飞离桌面，最终落在水平地面上。已知υ="3.0" m/s，m=0.10kg，l=1.4m，s=0.90m，物块与桌面间的动摩擦因数μ=0.25，不计空气阻力，重力加速度g取10m/s2。求：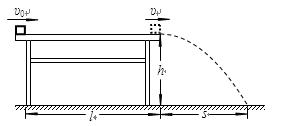
（1）桌面高h的大小；
（2）小物块的初速度大小v0。
如图12所示，固定在竖直平面内的光滑轨道，由一段斜直轨道和与之相切的圆形轨道连接而成，圆形轨道半径为R。一质量为m的小物块（可视为质点）从斜直轨道上的A点由静止开始下滑，然后沿圆形轨道运动。A点距轨道最低点的竖直高度为4R。已知重力加速度为g。求：
（1）小物块通过圆形轨道最高点C时速度v的大小；
（2）在最高点C时，轨道对小物块的作用力F的大小。
图甲为一研究电磁感应的实验装置示意图，其中电流传感器（相当于一只理想的电流表）能将各时刻的电流数据实时通过数据采集器传输给计算机，经计算机处理后在屏幕上同步显示出I-t图像．足够长光滑金属轨道电阻不计，倾角θ=30°．轨道上端连接有阻值R=1.0Ω的定值电阻，金属杆MN电阻r=0.5Ω，质量m=0.4kg，杆长 L=1.0m．在轨道区域加一垂直轨道平面向下的匀强磁场，让金属杆从图示位置由静止开始释放，此后计算机屏幕上显示出如图乙所示的I-t图像，设杆在整个运动过程中与轨道垂直，取g=10m/s2．试求：
（1）t=0.5s时电阻R的热功率；
（2）匀强磁场的磁感应强度B的大小；
（3）估算0~1.2s内通过电阻R的电荷量大小及在R上产生的焦耳热．