以“光盘”为主题的公益活动越来越受到社会的关注.某校为培养学生勤俭节约的习惯,随机抽查了部分学生(态度分为:赞成、无所谓、反对),并将抽查结果绘制成图1和图2(统计图不完整).请根据图中提供的信息,解答下列问题: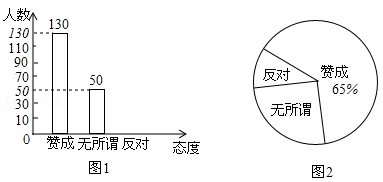
(1)此次抽样调查中,共抽查了多少名学生?
(2)将图1补充完整;
(3)根据抽样调查结果,请你估计该校3000名学生中有多少名学生持反对态度?
选取一个你喜欢的图形,然后将此图形放大,使放大后的图形的面积是原图形面积的4倍.
已知:△ABC∽△A′B′C′,它们的周长之差为20,面积比为4∶1,求△ABC和△A′B′C′的周长.
如图,梯形ABCD中,AB∥CD,AC、BD交于E,若S△DCE∶S△DCB=1∶3,求S△DCE∶S△ABD.
在比例尺为1∶50000的地图上,一块多边形地区的周长是72 cm,多边形的两个顶点A、B之间的距离是25 cm,求这个地区的实际边界长和A、B两地之间的实际距离.
如图,阳光透过窗口照到室内,在地面上留下2.7米宽的亮区,已知亮区一边到窗下的墙脚距离CE=8.7米,窗口高AB="1.8" 米,试求窗口下底与地面之间的距离BC的大小。