已知抛物线y= x2+1(如图所示).
x2+1(如图所示).
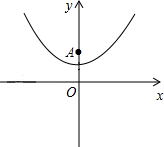
(1)填空:抛物线的顶点坐标是( , ),对称轴是 ;
(2)已知y轴上一点A(0,2),点P在抛物线上,过点P作PB⊥x轴,垂足为B.若△PAB是等边三角形,求点P的坐标;
(3)在(2)的条件下,点M在直线AP上.在平面内是否存在点N,使四边形OAMN为菱形?若存在,直接写出所有满足条件的点N的坐标;若不存在,请说明理由.
已知:如图,四边形ABCD中,AB>AD,AC平分∠DAB,∠B+∠D=180°.求证:CD=CB.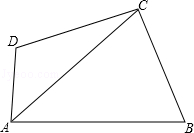
如图,边长为12cm的正方形纸片,点P为边BC的中点,折叠纸片使点A落在点P上,求AM的长.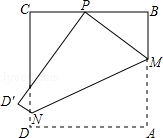
如图,在△MPN中,MP=NP,∠MPN=90°,S、P、Q在同一条直线上,NQ⊥PQ,MS⊥PS,垂足分别为Q、S,QS=8.4cm,NQ=2.1cm.试求出MS的长为多少cm.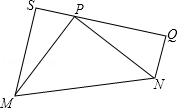
已知:如图,△ABC中,AD⊥BC于点D,AD=DC,∠FCD=∠BAD,点F在AD上,BF的延长线交AC于点E.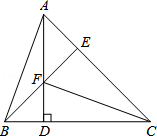
(1)求证:△ABD≌△CFD.
(2)求证:BE⊥AC;
(3)设CE的长为m,用含m的代数式表示AC+BF.
如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.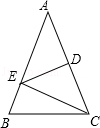
(1)求∠ECD的度数;
(2)若CE=5,求BC长.