(本小题满分10分)选修4-4:坐标系与参数方程
已知曲线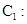
 (
(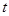 为参数),
为参数),
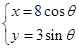 (
(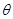 为参数).
为参数).
(1)化 ,
,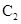 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)若 上的点
上的点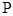 对应的参数为
对应的参数为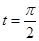 ,
,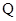 为
为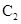 上的动点,求
上的动点,求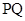 中点
中点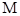 到直线
到直线
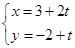 (
(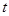 为参数)距离的最小值.
为参数)距离的最小值.
如图,已知三角形的顶点为 ,
,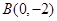 ,
,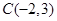 ,求:
,求:
(1)AB边上的中线CM所在直线的方程;
(2)求△ABC的面积.
一个几何体的三视图及其尺寸如下(单位:cm).
(1)画出该几何体的直观图,并说明图形名称(尺寸不作要求);
(2)求该几何体的表面积.
(1)直线在x轴上的截距是-1,在y轴上的截距是4,求此直线方程;
(2)求过直线x-2y+3=0和2x+y-4=0的交点,斜率为1 的直线方程。
如图,在三棱柱 中,
中,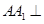 平面ABC,D、E分别是BC和
平面ABC,D、E分别是BC和 的中点,已知AB=AC=AA1=4,ÐBAC=90°.
的中点,已知AB=AC=AA1=4,ÐBAC=90°.
(1)求证: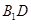 ⊥平面
⊥平面 ;
;
(2)求二面角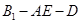 的余弦值;
的余弦值;
(3)求三棱锥 的体积.
的体积.
如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点, 是AC的中点,已知
是AC的中点,已知 ,
,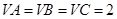 .
.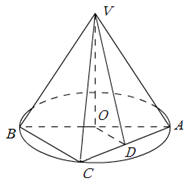
(1)求证:OD//平面VBC;
(2)求证:AC⊥平面VOD;
(3)求棱锥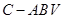 的体积.
的体积.