下列说法正确的是( )
| A.命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” |
B.已知 是R上的可导函数,则“ 是R上的可导函数,则“ ”是“ ”是“ 是函数 是函数 的极值点”的必要不充分条件 的极值点”的必要不充分条件 |
| C.命题“存在x∈R,使得x2+x+1<0”的否定是:“对任意x∈R,均有x2+x+1<0” |
D.命题“角 的终边在第一象限角,则 的终边在第一象限角,则 是锐角”的逆否命题为真命题 是锐角”的逆否命题为真命题 |
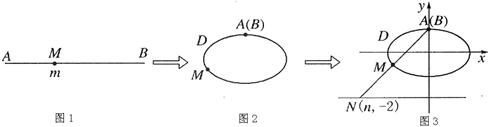
下图展示了一个由区间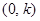 (其中
(其中 为一正实数)到实数集R上的映射过程:区间
为一正实数)到实数集R上的映射过程:区间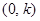 中的实数
中的实数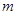 对应线段
对应线段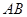 上的点
上的点 ,如图1;将线段
,如图1;将线段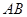 围成一个离心率为
围成一个离心率为 的椭圆,使两端点
的椭圆,使两端点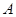 、
、 恰好重合于椭圆的一个短轴端点,如图2 ;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在
恰好重合于椭圆的一个短轴端点,如图2 ;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在 轴上,已知此时点
轴上,已知此时点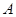 的坐标为
的坐标为 ,如图3,在图形变化过程中,图1中线段
,如图3,在图形变化过程中,图1中线段 的长度对应于图3中的椭圆弧ADM的长度.图3中直线
的长度对应于图3中的椭圆弧ADM的长度.图3中直线 与直线
与直线 交于点
交于点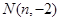 ,则与实数
,则与实数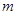 对应的实数就是
对应的实数就是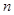 ,记作
,记作 ,
,
现给出下列5个命题
① ; ②函数
; ②函数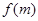 是奇函数;③函数
是奇函数;③函数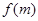 在
在 上单调递增; ④.函数
上单调递增; ④.函数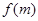 的图象关于点
的图象关于点 对称;⑤函数
对称;⑤函数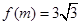 时AM过椭圆的右焦点.其中所有的真命题是:()
时AM过椭圆的右焦点.其中所有的真命题是:()
| A.①③⑤ | B.②③④ | C.②③⑤ | D.③④⑤ |
将一枚骰子先后抛掷两次,若第一次朝上一面的点数为 ,第二次朝上一面的点数为
,第二次朝上一面的点数为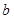 ,则函数
,则函数 在
在 上为减函数的概率是()
上为减函数的概率是()
A.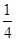 |
B.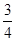 |
C.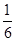 |
D. |
在平面直角坐标系中,横坐标和纵坐标均为整数的点称为格点,如果函数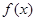 的图象恰好通过
的图象恰好通过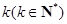 个格点,则称函数
个格点,则称函数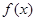 为
为 阶格点函数. 给出下列4个函数:
阶格点函数. 给出下列4个函数:
① ;②
;②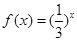 ;③
;③ ;④
;④ .
.
其中是一阶格点函数的是()
| A.①③ | B.②③ | C.③④ | D.①④ |
若数列 满足
满足 ,则
,则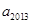 的值为()
的值为()
| A.2 | B. |
C.1 | D. |
实数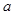 的值由右上面程序框图算出,则二项式
的值由右上面程序框图算出,则二项式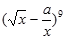 展开式的常数项为()
展开式的常数项为()
A.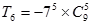 |
B.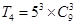 |
C.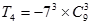 |
D.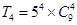 |
