(本小题满分10分)在平面直角坐标系中,曲线C1 的参数方程为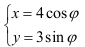 (ϕ为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2cosθ。
(ϕ为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2cosθ。
(1)求曲线C2的直角坐标方程;
(2)已知点M是曲线C1上任意一点,点N是曲线C2上任意一点,求|MN|的取值范围。
已知数列 的前
的前 项和
项和 ,数列
,数列 满足
满足
 .
.
(1)求数列 的通项
的通项 ;
;
(2)求数列 的通项
的通项 ;
;
(3)若 ,求数列
,求数列 的前
的前 项和
项和 .
.
如图,已知 为平行四边形,
为平行四边形, ,
, ,
, ,点
,点 在
在 上,
上, ,
, ,
, 与
与 相交于
相交于 .现将四边形
.现将四边形 沿
沿 折起,使点
折起,使点 在平面
在平面 上的射影恰在直线
上的射影恰在直线 上.
上.
(1)求证: 平面
平面 ;
;
(2)求折后直线 与平面
与平面 所成角的余弦值.
所成角的余弦值.
已知关于 的一元二次函数
的一元二次函数 ,设集合
,设集合 ,分别从集合P和Q中随机取一个数作为
,分别从集合P和Q中随机取一个数作为 和
和
(1)求函数 有零点的概率;
有零点的概率;
(2)求函数 在区间
在区间 上是增函数的概率。
上是增函数的概率。
已知数列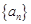 满足:
满足: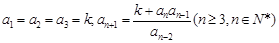 其中
其中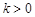 ,数列
,数列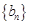 满足:
满足: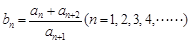
(1)求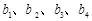 ;
;
(2)求数列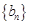 的通项公式;
的通项公式;
(3)是否存在正数k,使得数列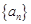 的每一项均为整数,如果不存在,说明理由,如果存在,求出所有的k.
的每一项均为整数,如果不存在,说明理由,如果存在,求出所有的k.
已知函数
(1)若方程 内有两个不等的实根,求实数m的取值范围;(e为自然对数的底数)
内有两个不等的实根,求实数m的取值范围;(e为自然对数的底数)
(2)如果函数 的图象与x轴交于两点
的图象与x轴交于两点 、
、 且
且 .求证:
.求证: (其中正常数
(其中正常数 ).
).