（本小题满分12分）已知函数
=lnx。
（1）求函数g（x）=f（x）+mx2−4x在定义域内单调递增，求实数m的取值范围；
（2）若b>a>0，求证：f（b）−f（a）>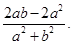 
（本小题满分12分）已知函数
，
.
（Ⅰ）若函数
在定义域上是增函数，求a的取值范围；
（Ⅱ）求
的最大值.
（本小题满分12分）已知圆
，点
，以线段AB为直径的圆内切于圆
，记点B的轨迹为
.
（Ⅰ）求曲线的方程；
（Ⅱ）直线AB交圆于C，D两点，当B为CD中点时，求直线AB的方程.
（本小题满分12分）如图，在斜三棱柱
中，侧面
与侧面
都是菱形，
，
.
（Ⅰ）求证：
；
（Ⅱ）若
，求四棱锥
的体积.
（本小题满分12分）
为了研究某种细菌在特定环境下，随时间变化繁殖情况，得如下实验数据：
| 天数t（天） |
3 |
4 |
5 |
6 |
7 |
| 繁殖个数y（千个） |
2.5 |
3 |
4 |
4.5 |
6 |
（Ⅰ）求y关于t的线性回归方程；
（Ⅱ）利用（Ⅰ）中的回归方程，预测
时，细菌繁殖个数.
附：回归直线的斜率和截距的最小二乘法估计公式分别为：
，
.
（本小题满分12分）设数列
的前n项和为
，满足
，且
.
（Ⅰ）求的通项公式；
（Ⅱ）若
成等差数列，求证：
成等差数列.