计算：（1）－8－622－9．；（2）；（3）－8÷（

定义：

数学活动课上，李老师给出如下定义：如果一个三角形有一边上的中线等于这条边的一半，那么称这个三角形为“智慧三角形”．

理解：

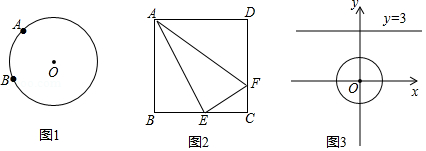
（1）如图1，已知 $A$ 、 $B$ 是 $⊙ O$ 上两点，请在圆上找出满足条件的点 $C$ ，使 $ΔABC$ 为“智慧三角形”（画出点 $C$ 的位置，保留作图痕迹）；

（2）如图2，在正方形 $ABCD$ 中， $E$ 是 $BC$ 的中点， $F$ 是 $CD$ 上一点，且 $CF = \frac{1}{4} CD$ ，试判断 $ΔAEF$ 是否为“智慧三角形”，并说明理由；

运用：

（3）如图3，在平面直角坐标系 $xOy$ 中， $⊙ O$ 的半径为1，点 $Q$ 是直线 $y = 3$ 上的一点，若在 $⊙ O$ 上存在一点 $P$ ，使得 $ΔOPQ$ 为“智慧三角形”，当其面积取得最小值时，直接写出此时点 $P$ 的坐标．

某公司开发出一款新的节能产品，该产品的成本价为6元 $/$ 件，该产品在正式投放市场前通过代销点进行了为期一个月（30天）的试销售，售价为8元 $/$ 件，工作人员对销售情况进行了跟踪记录，并将记录情况绘成图象，图中的折线 $ODE$ 表示日销售量 $y$ （件）与销售时间 $x$ （天）之间的函数关系，已知线段 $DE$ 表示的函数关系中，时间每增加1天，日销售量减少5件．

（1）第24天的日销售量是　　件，日销售利润是　　元．

（2）求 $y$ 与 $x$ 之间的函数关系式，并写出 $x$ 的取值范围；

（3）日销售利润不低于640元的天数共有多少天？试销售期间，日销售最大利润是多少元？

如图，在 $ΔABC$ 中， $AB = AC$ ，以 $AB$ 为直径的 $⊙ O$ 与边 $BC$ 、 $AC$ 分别交于 $D$ 、 $E$ 两点，过点 $D$ 作 $DF ⊥ AC$ ，垂足为点 $F$ ．

（1）求证： $DF$ 是 $⊙ O$ 的切线；

（2）若 $AE = 4$ ， $\cos A = \frac{2}{5}$ ，求 $DF$ 的长．

小慧根据学习函数的经验，对函数 $y = | x - 1 |$ 的图象与性质进行了探究．下面是小慧的探究过程，请补充完成：

（1）函数 $y = | x - 1 |$ 的自变量 $x$ 的取值范围是　　；

（2）列表，找出 $y$ 与 $x$ 的几组对应值．

$x$	$\dots$	$- 1$	0	1	2	3	$\dots$
$y$	$\dots$	b	1	0	1	2	$\dots$

其中， $b =$ 　　；

（3）在平面直角坐标系 $xOy$ 中，描出以上表中各对对应值为坐标的点，并画出该函数的图象；

（4）写出该函数的一条性质：　　．

咸宁市某中学为了解本校学生对新闻、体育、动画、娱乐四类电视节目的喜爱情况，随机抽取了部分学生进行问卷调查，根据调查结果绘制了如图所示的两幅不完整统计图，请你根据图中信息解答下列问题：

（1）补全条形统计图，“体育”对应扇形的圆心角是　　度；

（2）根据以上统计分析，估计该校2000名学生中喜爱“娱乐”的有　　人；

（3）在此次问卷调查中，甲、乙两班分别有2人喜爱新闻节目，若从这4人中随机抽取2人去参加“新闻小记者”培训，请用列表法或画树状图的方法求所抽取的2人来自不同班级的概率．