如图,设抛物线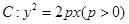 的焦点为F,过点F的直线l1交抛物线C于A,B两点,且
的焦点为F,过点F的直线l1交抛物线C于A,B两点,且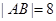 ,线段AB的中点到y轴的距离为3.
,线段AB的中点到y轴的距离为3.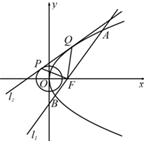
(Ⅰ)求抛物线C的方程;
(Ⅱ)若直线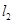 与圆
与圆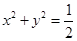 切于点P,与抛物线C切于点Q,求
切于点P,与抛物线C切于点Q,求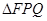 的面积.
的面积.
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛. 为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计. 请你根据尚未完成并有局部污损的频率分布表和频数分布直方图,解答下列问题:
(1)填充频率分布表的空格(将答案直接填在表格内);
| 分组 |
频数 |
频率 |
| 50.5~60.5 |
4 |
0.08 |
| 60.5~70.5 |
0.16 |
|
| 70.5~80.5 |
10 |
|
| 80.5~90.5 |
16 |
0.32 |
| 90.5~100.5 |
||
| 合计 |
50 |
(2)补全频数条形图;
(3)若成绩在75.5~85.5分的学生为二等奖,问获得二等奖的学生约为多少人。
画出求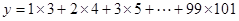 值的一个算法的程序框图
值的一个算法的程序框图
已知向量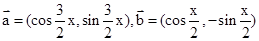 ,且x∈[0,
,且x∈[0, ],求
],求
(1) ;
;
(2)若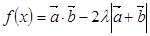 的最小值是
的最小值是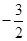 ,求实数
,求实数 的值。
的值。
已知函数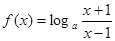
 .
.
(1)判断函数 的奇偶性;
的奇偶性;
(2)判断函数 在
在 上的单调性,并给出证明;
上的单调性,并给出证明;
(3)当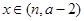 时,函数
时,函数 的值域是
的值域是 ,求实数
,求实数 与
与 的值;
的值;
已知函数 其中
其中 ,
,
(I)若 求
求 的值;
的值;
(Ⅱ)在(I)的条件下,若函数 的图像的相邻两条对称轴之间的距离等于
的图像的相邻两条对称轴之间的距离等于 ,求函数
,求函数 的解析式;并求最小正实数
的解析式;并求最小正实数 ,使得函数
,使得函数 的图像象左平移
的图像象左平移 个单位所对应的函数是偶函数。
个单位所对应的函数是偶函数。