把正奇数数列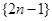 中的数按上小下大、左小右大的原则排成如图的三角形数表:
中的数按上小下大、左小右大的原则排成如图的三角形数表:
设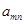
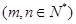 是位于这个三角形数表中从上往下数第m行、从左往右数第n个数.
是位于这个三角形数表中从上往下数第m行、从左往右数第n个数.
(1)求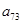 ;
;
(2)若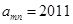 ,求m,n的值;
,求m,n的值;
(3)已知函数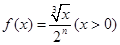 ,若记三角形数表中从上往下数第n行各数的和为bn,求数列{f(bn)}的前n项和
,若记三角形数表中从上往下数第n行各数的和为bn,求数列{f(bn)}的前n项和 .
.
(本小题满分12分)已知函数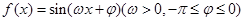 在
在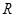 上是偶函数,其图象关于直线
上是偶函数,其图象关于直线 对称,且在区间
对称,且在区间 上是单调函数,求
上是单调函数,求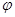 和
和 的值.
的值.
(本小题满分12分)
(Ⅰ)已知函数 在
在 上具有单调性,求实数
上具有单调性,求实数 的取值范围;
的取值范围;
(Ⅱ)已知向量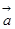 、
、 、
、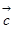 两两所成的角相等,且
两两所成的角相等,且 ,
, ,
,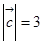 ,求
,求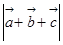 .
.
(本小题满分12分)已知函数 .
.
(Ⅰ)求满足 时的
时的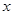 的集合;
的集合;
(Ⅱ)当 时,求函数
时,求函数 的最值.
的最值.
(本小题12分)为了丰富学生的课余生活,促进校园文化建设,我校高二年级通过预赛选出了6个班(含甲、乙)进行经典美文颂读比赛决赛.决赛通过随机抽签方式决定出场顺序.
求:(1)甲、乙两班恰好在前两位出场的概率;
(2)决赛中甲、乙两班之间的班级数记为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
(本小题满分14分)
以椭圆 :
: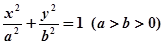 的中心
的中心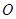 为圆心,
为圆心,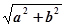 为半径的圆称为该椭圆的“准圆”.设椭圆
为半径的圆称为该椭圆的“准圆”.设椭圆 的左顶点为
的左顶点为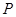 ,左焦点为
,左焦点为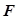 ,上顶点为
,上顶点为 ,且满足
,且满足 ,
,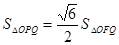 .
.
(Ⅰ)求椭圆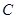 及其“准圆”的方程;
及其“准圆”的方程;
(Ⅱ)若椭圆 的“准圆”的一条弦
的“准圆”的一条弦 (不与坐标轴垂直)与椭圆
(不与坐标轴垂直)与椭圆 交于
交于 、
、 两点,试证明:当
两点,试证明:当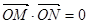 时,试问弦
时,试问弦 的长是否为定值,若是,求出该定值;若不是,请说明理由.
的长是否为定值,若是,求出该定值;若不是,请说明理由.