(本小题满分12分)
设点 ,
,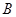 的坐标分别为
的坐标分别为 ,
, ,直线
,直线 ,
, 相交于点
相交于点 ,且它们的斜率之积是
,且它们的斜率之积是 .
.
(1)求点 的轨迹
的轨迹 的方程;
的方程;
(2) ,
, ,
, 为曲线
为曲线 上的三个动点,
上的三个动点,  在第一象限,
在第一象限,  ,
, 关于原点对称,且
关于原点对称,且 ,问
,问 的面积是否存在最小值?若存在,求出此时
的面积是否存在最小值?若存在,求出此时 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
已知数列{ }、{
}、{ }满足:
}满足: 。
。
(Ⅰ)求 ;
;
(Ⅱ)设 ,求数列
,求数列 的通项公式;
的通项公式;
(Ⅲ)设 ,不等式
,不等式 恒成立时,求实数
恒成立时,求实数 的取值范围。
的取值范围。
已知函数 ,其定义域为
,其定义域为 (
( ),设
),设 。
。
(Ⅰ)试确定 的取值范围,使得函数
的取值范围,使得函数 在
在 上为单调函数;
上为单调函数;
(Ⅱ)试判断 的大小并说明理由;
的大小并说明理由;
(Ⅲ)求证:对于任意的 ,总存在
,总存在 ,满足
,满足 ,并确定这样的
,并确定这样的 的个数。
的个数。
设 为正实数,
为正实数, ,
, ,
, 。
。
(Ⅰ)如果 ,则是否存在以
,则是否存在以 为三边长的三角形?请说明理由;
为三边长的三角形?请说明理由;
(Ⅱ)对任意的正实数 ,试探索当存在以
,试探索当存在以 为三边长的三角形时
为三边长的三角形时 的取值范围。
的取值范围。
已知 为坐标原点,
为坐标原点, ,
, 。
。
(Ⅰ)求 的单调递增区间;
的单调递增区间;
(Ⅱ)若 的定义域为
的定义域为 ,值域为
,值域为 ,求
,求 的值。
的值。
某研究机构准备举行一次数学新课程研讨会,共邀请50名一线教师参加,使用不同版本教材的教师人数如下表所示:
| 版本 |
人教A版 |
人教B版 |
苏教版 |
北师大版 |
| 人数 |
20 |
15 |
5 |
10 |
(Ⅰ)从这50名教师中随机选出2名,求2人所使用版本相同的概率;
(Ⅱ)若随机选出2名使用人教版的教师发言,设使用人教A版的教师人数为 ,求随机变量
,求随机变量 的分布列和数学期望。
的分布列和数学期望。