(本小题满分12分)
为了调查某高中学生每天的睡眠时间,现随机对20名男生和20名女生进行问卷调查,结果如下:
女生:
| 睡眠时间(小时) |
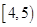 |
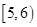 |
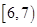 |
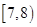 |
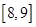 |
| 人数 |
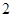 |
 |
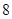 |
 |
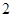 |
男生:
| 睡眠时间(小时) |
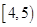 |
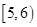 |
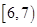 |
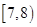 |
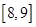 |
| 人数 |
 |
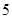 |
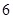 |
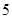 |
 |
(1)现把睡眠时间不足5小时的定义为“严重睡眠不足”,从睡眠时间不足6小时的女生中随机抽取3人,求此3人中恰有一人为“严重睡眠不足”的概率;
(2)完成下面2×2列联表,并回答是否有90%的把握认为“睡眠时间与性别有关”?
| |
睡眠时间少于7小时 |
睡眠时间不少于7小时 |
合计 |
| 男生 |
|
|
|
| 女生 |
|
|
|
| 合计 |
|
|
|
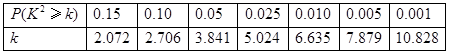
(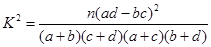 ,其中
,其中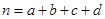 )
)
如图,在三棱柱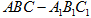 中,四边形
中,四边形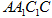 是边长为4的正方形,平面
是边长为4的正方形,平面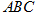 ⊥平面
⊥平面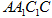 ,
,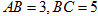 .
.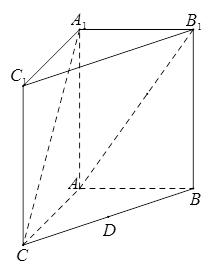
(Ⅰ)求证: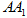 ⊥平面
⊥平面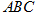 ;
;
(Ⅱ)若点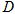 是线段
是线段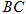 的中点,请问在线段
的中点,请问在线段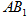 是否存在点
是否存在点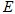 ,使得
,使得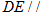 面
面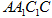 ?若存在,请说明点
?若存在,请说明点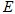 的位置,若不存在,请说明理由;
的位置,若不存在,请说明理由;
(Ⅲ)求二面角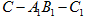 的大小.
的大小.
已知△ABC的顶点C在直线3x﹣y=0上,顶点A、B的坐标分别为(4,2),(0,5).
(Ⅰ)求过点A且在x,y轴上的截距相等的直线方程;
(Ⅱ)若△ABC的面积为10,求顶点C的坐标.
已知圆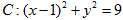 内有一点
内有一点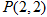 ,过点
,过点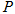 作直线
作直线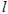 交圆于
交圆于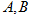 两点.
两点.
(1)当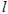 经过圆心
经过圆心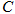 时,求直线
时,求直线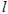 的方程;
的方程;
(2)当弦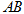 被点
被点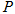 平分时,写出直线
平分时,写出直线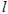 的方程和弦
的方程和弦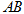 的长.
的长.
如图:已知四棱锥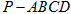 中,
中,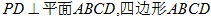 是正方形,E是
是正方形,E是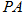 的中点,求证:
的中点,求证: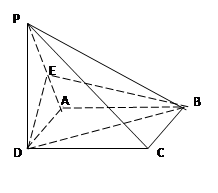
(1)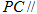 平面
平面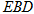
(2)平面PBC⊥平面PCD
已知圆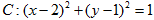 .求过点
.求过点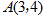 的圆
的圆 的切线方程.
的切线方程.