已知{an}为等差数列,且a3=-6,a6=0.
(1)求{an}的通项公式;
(2)若等比数列{bn}满足b1=-8,b2=a1+a2+a3,求{bn}的前n项和公式.
已知函数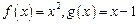 .
.
(1)若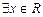 使
使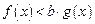 ,求实数
,求实数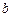 的取值范围;
的取值范围;
(2)设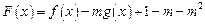 ,且
,且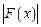 在
在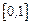 上单调递增,求实数
上单调递增,求实数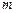 的取值范围.
的取值范围.
已知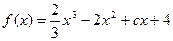 ,
,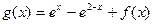 ,
,
(1)若f(x)在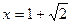 处取得极值,试求c的值和f(x)的单调增区间;
处取得极值,试求c的值和f(x)的单调增区间;
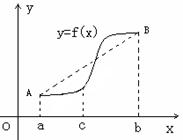
(2)如右图所示,若函数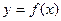 的图象在
的图象在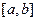 连续光滑,试猜想拉格朗日中值定理:即一定存在
连续光滑,试猜想拉格朗日中值定理:即一定存在 使得
使得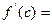 ?(用含有a,b,f(a),f(b)的表达式直接回答)
?(用含有a,b,f(a),f(b)的表达式直接回答)
(3)利用(2)证明:函数y=g(x)图象上任意两点的连线斜率不小于2e-4.
(本小题满分14分)已知10件产品中有3件是次品.
(I)任意取出3件产品作检验,求其中至少有1件是次品的概率;
(II)为了保证使3件次品全部检验出的概率超过0.6,最少应抽取几件产品作检验?
已知向量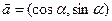 ,
, 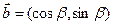 ,
, 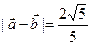 .
.
(Ⅰ)求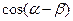 的值;
的值;
(Ⅱ)若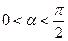 ,
, 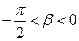 , 且
, 且 , 求
, 求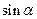 .
.
(本小题满分12分)已知实数 ,函数
,函数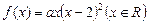 .
.
(Ⅰ)若函数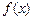 有极大值32,求实数
有极大值32,求实数 的值;(Ⅱ)若对
的值;(Ⅱ)若对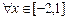 ,不等式
,不等式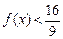 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.