(本小题满分12分)已知实数 ,函数
,函数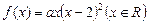 .
.
(Ⅰ)若函数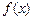 有极大值32,求实数
有极大值32,求实数 的值;(Ⅱ)若对
的值;(Ⅱ)若对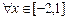 ,不等式
,不等式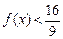 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
如图,四边形ABCD中,AB⊥AD,AD∥BC,AD=6,BC=4,AB=3,点E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使平面ABEF 平面EFDC,设AD中点为P.
平面EFDC,设AD中点为P.
(Ⅰ)当E为BC中点时,求证:CP∥平面ABEF;
(Ⅱ)设BE=x,当x为何值时,三棱锥A-CDF的体积有最大值?并求出这个最大值.
已知函数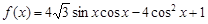 .
.
(Ⅰ)求函数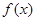 在
在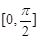 上的值域;
上的值域;
(Ⅱ)若对于任意的 ,不等式
,不等式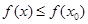 恒成立,求
恒成立,求 .
.
某电视台2012年举办了“中华好声音”大型歌手选秀活动,过程分为初赛、复赛和决赛,经初赛进入复赛的40名选手被平均分成甲、乙两个班。下面是根据这40名选手参加复赛时获得的100名大众评审的支持票数制成的茎叶图: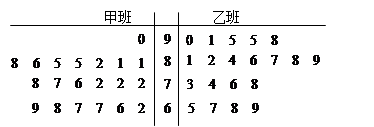
赛制规定:参加复赛的40名选手中,获得的支持票数排在前5名的选手可进入决赛,若第5名出现并列,则一起进入决赛;另外,票数不低于95票的选手在决赛时拥有“优先挑战权”。
(Ⅰ)分别求出甲、乙两班的大众评审的支持票数的中位数、众数与极差;
从进入决赛的选手中随机抽出3名,求其中恰有1名拥有“优先挑战权”的概率.
已知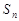 为数列
为数列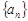 的前
的前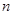 项和,且
项和,且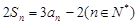 .
.
(Ⅰ)求数列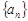 的通项公式;
的通项公式;
(Ⅱ)若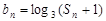 ,求数列
,求数列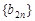 的前n项和
的前n项和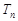 .
.
已知函数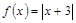 ,
,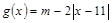 , 若
, 若
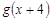 恒成立,实数
恒成立,实数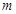 的最大值为
的最大值为 .
.
(1)求实数 .
.
(2)已知实数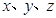 满足
满足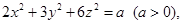 且
且 的最大值是
的最大值是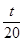 ,求
,求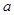 的值.
的值.