如图,四边形ABCD中,AB⊥AD,AD∥BC,AD=6,BC=4,AB=3,点E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使平面ABEF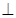 平面EFDC,设AD中点为P.
平面EFDC,设AD中点为P.
(Ⅰ)当E为BC中点时,求证:CP∥平面ABEF;
(Ⅱ)设BE=x,当x为何值时,三棱锥A-CDF的体积有最大值?并求出这个最大值.
.围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元)。
(Ⅰ)将y表示为x的函数
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,求出最小总费用。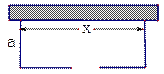
已知关于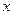 的不等式
的不等式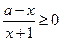 的解集为
的解集为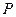 ,不等式
,不等式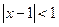 的解集为
的解集为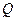
(1)若 ,求
,求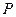 ;(2)若
;(2)若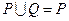 ,求正数
,求正数 的取值范围。
的取值范围。
(本小题满分13分)
设函数 .
.
(1)求证:不论 为何实数
为何实数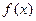 总为增函数;
总为增函数;
(2)确定 的值,使
的值,使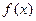 为奇函数及此时
为奇函数及此时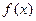 的值域.
的值域.
(本小题满分13分)
为了预防甲型流感,某学校对教室用药熏消毒法进行消毒. 已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为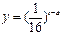 (a为常数),如图所示,根据图中提供的信息,回答下列问题:
(a为常数),如图所示,根据图中提供的信息,回答下列问题:
(1)求从药物释放开始,每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式;
(2)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室,那从药物释放开始,至少需要经过多少小时后,学生才能回到教室.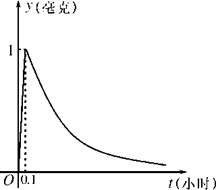
(本小题满分12分)
设函数 ,如果
,如果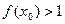 ,求
,求 的取值范围.
的取值范围.