如图,在直角坐标系xOy中,一次函数y=k1x+b的图象与反比例函数y=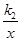 的图象交于A(1,4)、B(3,m)两点.
的图象交于A(1,4)、B(3,m)两点.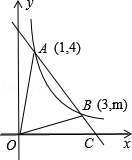
(1)求一次函数的解析式;
(2)求△AOB的面积.
如图,梯形ABCD中,AB‖CD,且AB∶CD=4∶3,E是CD的中点,AC与BE交于点F. 
(1)求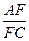 的值;
的值;
(2)若 ,请用
,请用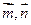 来表示
来表示
已知二次函数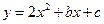 的图像经过点
的图像经过点 与
与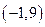 .
.
(1)求此函数的解析式;
(2)用配方法求此函数图像的顶点坐标.
如图,在△ABC中,BC=9,AB ,∠ABC=
,∠ABC= .
. 
(1)求△ABC的面积;
(2)求cos∠C的值.
如图,直角梯形ABCD中,AB∥DC,∠DAB=90°,AD=2DC=4,AB=6.动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与折线A-C-B的交点为Q.点M运动的时间为t(秒).
(1)当 时,求线段
时,求线段 的长;
的长;
(2)点M在线段AB上运动时,是否可以使得以C、P、Q为顶点的三角形为直角三角形,若可以,请直接写出t的值(不需解题步骤);若不可以,请说明理由.
(3)若△PCQ的面积为y,请求y关于出t 的函数关系式及自变量的取值范围;
如图,已知抛物线与 轴交于点
轴交于点 ,
, ,与y轴交于点
,与y轴交于点 .
.
(1)求抛物线的解析式及其顶点D的坐标;
(2)设直线CD交 轴于点E.在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由
轴于点E.在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由