如图,直径为10的⊙O经过原点O,并且与x轴、y轴分别交于A、B两点,线段OA、OB(OA>OB)的长分别是方程x2+kx+48=0的两根。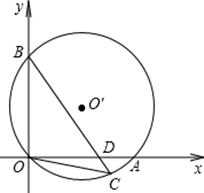
(1)求线段OA、OB的长;
(2)已知点C在劣弧OA上,连结BC交OA于D,当OC2=CD·CB时,求C点的坐标;
(3)在⊙O上是否存在点P,使S△POD=S△ABD.若存在,求出点P的坐标;若不存在,请说明理由.
如图,一次函数 的图象与反比例函数
的图象与反比例函数 的图象相交于A(2,1),B两点.
的图象相交于A(2,1),B两点.
(1)求出反比例函数与一次函数的表达式;
(2)请直接写出B点的坐标,并指出使反比例函数值大于一次函数值的x的取值范围.
某校为了增强学生对中华优秀传统文化的理解,决定购买一批相关的书籍.据了解,经典著作的单价比传说故事的单价多8元,用12000元购买经典著作与用8000元购买传说故事的本数相同,这两类书籍的单价各是多少元?
小华为了测量楼房AB的高度,他从楼底的B处沿着斜坡向上行走20m,到达坡顶D处.已知斜坡的坡角为15°.(以下计算结果精确到0.1m)
(1)求小华此时与地面的垂直距离CD的值;
(2)小华的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45°,求楼房AB的高度.
在“阳光体育”活动时间,小英、小丽、小敏、小洁四位同学进行一次羽毛球单打比赛,要从中选出两位同学打第一场比赛.
(1)若已确定小英打第一场,再从其余三位同学中随机选取一位,求恰好选中小丽同学的概率;
(2)用画树状图或列表的方法,求恰好选中小敏、小洁两位同学进行比赛的概率.
如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,且AE∥CD,CE∥AB.
(1)四边形ADCE是菱形;
(2)若∠B=60°,BC=6,求菱形ADCE的高.(计算结果保留根号)