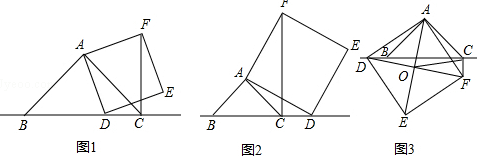
已知,在△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一动点(点D不与点B,C重合).以AD为边做正方形ADEF,连接CF
(1)如图1当点D在线段BC上时.求证CF+CD=BC;
(2)如图2,当点D在线段BC的延长线上时,其他条件不变,请直接写出CF,BC,CD三条线段之间的关系;
(3)如图3,当点D在线段BC的反向延长线上时,且点A,F分别在直线BC的两侧,其他条件不变; ①请直接写出CF,BC,CD三条线段之间的关系;
②若正方形ADEF的边长为2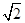 ,对角线AE,DF相交于点O,连接OC.求OC的长度.
,对角线AE,DF相交于点O,连接OC.求OC的长度.
如图,已知PA、PB切⊙O于A、B两点,PO=4cm,∠APB=60°,求阴影部分的周长.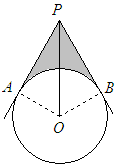
如图,⊙O的半径为17cm,弦AB∥CD,AB=30cm,CD=16cm,圆心O位于AB、CD的上方,求AB和CD间的距离.
操作题:如图,⊙O是△ABC的外接圆,AB=AC,P是⊙O上一点.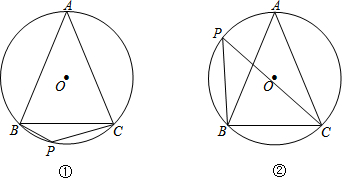
(1)请你只用无刻度的直尺,分别画出图①和图②中∠P的平分线;
(2)结合图②,说明你这样画的理由.
一只不透明的袋子中装有4个大小、质地都相同的乒乓球,球面上分别标有数字1、-2、3、-4,搅匀后先从中摸出一个球(不放回),再从余下的3个球中摸出1个球.
(1)用树状图列出所有可能出现的结果;
(2)求2次摸出的乒乓球球面上数字的积为偶数的概率.
如图,学校打算用16 m 的篱笆围成一个长方形的生物园饲养小兔,生物园的一面靠墙(如下图),面积是30 m2.求生物园的长和宽.