(本小题12分)某人在一山坡P处观看对面山项上的一座铁塔,如图所示,塔高 (米),塔所在的山高
(米),塔所在的山高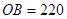 (米),
(米), (米),图中所示的山坡可视为直线
(米),图中所示的山坡可视为直线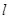 且点
且点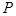 在直线
在直线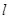 上,
上, 与水平地面的夹角为
与水平地面的夹角为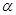 ,
, ,试问此人距水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高)
,试问此人距水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高)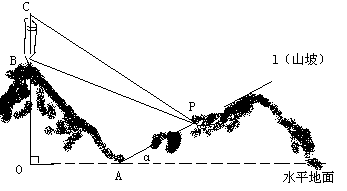
如图,已知椭圆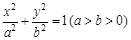 的右顶点为A(2,0),点P(2e,
的右顶点为A(2,0),点P(2e, )在椭圆上(e为椭圆的离心率).
)在椭圆上(e为椭圆的离心率).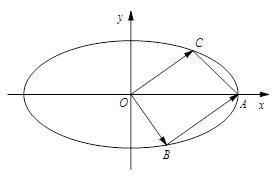
(1)求椭圆的方程;
(2)若点B,C(C在第一象限)都在椭圆上,满足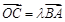 ,且
,且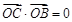 ,求实数λ的值.
,求实数λ的值.
甲、乙两地相距1000 ,货车从甲地匀速行驶到乙地,速度不得超过80
,货车从甲地匀速行驶到乙地,速度不得超过80 ,已知货车每小时的运输成本(单位:元)由可变成本和固定成本组成,可变成本是速度平方的
,已知货车每小时的运输成本(单位:元)由可变成本和固定成本组成,可变成本是速度平方的 倍,固定成本为a元.
倍,固定成本为a元.
(1)将全程运输成本y(元)表示为速度v( )的函数,并指出这个函数的定义域;
)的函数,并指出这个函数的定义域;
(2)为了使全程运输成本最小,货车应以多大的速度行驶?
如图,在四棱锥P-ABCD中,四边形ABCD是矩形,平面PCD⊥平面ABCD,M为PC中点.求证:
(1)PA∥平面MDB;
(2)PD⊥BC.
在△ABC中,设角A,B,C的对边分别为a,b,c,且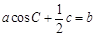 .
.
(1)求角A的大小;
(2)若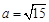 ,
,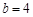 ,求边c的大小.
,求边c的大小.
设 为随机变量,从棱长为1的正方体ABCD-A1B1C1D1的八个顶点中任取四个点,当四点共面时,
为随机变量,从棱长为1的正方体ABCD-A1B1C1D1的八个顶点中任取四个点,当四点共面时, =0,当四点不共面时,
=0,当四点不共面时, 的值为四点组成的四面体的体积.
的值为四点组成的四面体的体积.
(1)求概率P( =0);
=0);
(2)求 的分布列,并求其数学期望E (
的分布列,并求其数学期望E ( ).
).