甲、乙两车均沿同一平直公路同向行驶。开始时,甲车在乙车前方s0=75m处。甲车始终以v1=10m/s的速度匀速运动。乙车作初速度为零,加速度a=2m/s2的匀加速直线运动。求:
(1)乙车追上甲车之前,两车之间的最大距离sm;
(2)经过多少时间t,乙车追上甲车?
(3)乙车一追上甲车,乙车就立即刹车,减速过程加速度大小a'=5m/s2,则再经过多少时间t',甲、乙两车再次相遇。(设乙车能从甲车旁通过,不发生相撞)
如图所示,在光滑水平面上有两个并排放置的木块A和B,已知mA=0.5kg,mB=0.3kg,有一质量为mC=0.1kg的小物块C以20m/s的水平速度滑上A表面,由于C和A、B间有摩擦,C滑到B表面上时最终与B共同以2.5m/s的速度运动,求: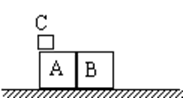
(1)木块A的最终速度;
(2)C滑离A木块的瞬时速度。
(注:衰变生成的新核均由X来表示)
(1)写出所给放射性元素的β衰变方程: (铋核)
(铋核)
(2)写出所给放射性元素的α衰变方程: (钍核)
(钍核)
(3)已知钍234的半衰期是24天,1g钍经过120天后还剩多少?
如图所示的竖直平面内,相距为d的不带电平行金属板M、N水平固定放置,与灯泡L、开关S组成回路并接地,上极板M与其上方空间的D点相距h,灯泡L的额定功率与电压分别为PL、UL。带电量为q的小物体以水平向右的速度v0从D点连续发射,落在M板其电荷立即被吸收,M板吸收一定电量后闭合开关S,灯泡能维持正常发光。设小物体视为质点,重力加速度为g,金属板面积足够大,M板吸收电量后在板面均匀分布,M、N板间形成匀强电场,忽略带电小物体间的相互作用。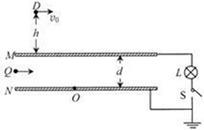
(1)初始时带电小物体落在M板上的水平射程为多少?
(2)单位时间发射小物体的个数为多少?
(3)闭合开关S后,带电粒子Q以水平速度从匀强电场左侧某点进入电场,并保持速度穿过M、N板之间。现若在M、N板间某区域加上方向垂直于纸面的匀强磁场,使Q在纸面内无论从电场左侧任何位置以某水平速度进入,都能到达N板上某定点O,求所加磁场区域为最小时的几何形状及位置。
如图所示,AKD为竖直平面内固定的光滑绝缘轨道,轨道间均平滑连接,AK段水平,其间分布有一水平向右的匀强电场I。PQ为同一竖直面内的固定光滑水平轨道。自D点向右宽度L=0.7m的空间,分布有水平向右、场强大小E=1.4×105N/C的匀强电场II。质量m2=0.1kg、长度也为L的不带电绝缘平板,静止在PQ上并恰好处于电场II中,板的上表面与弧形轨道相切于D点。AK轨道上一带正电的小物体从电场I的左边界由静止开始运动,并在D点以速度v=1m/s滑上平板。已知小物体的质量m1=10-2kg,电荷量q=+10-7C,与平板间的动摩擦因数 ,AK与D点的垂直距离为h=0.3m,小物体离开电场II时速度比平板的大、小物体始终在平板上。设小物体电荷量保持不变且视为质点,取g=10m/s2。求:
,AK与D点的垂直距离为h=0.3m,小物体离开电场II时速度比平板的大、小物体始终在平板上。设小物体电荷量保持不变且视为质点,取g=10m/s2。求:
(1)电场I左右边界的电势差;
(2)小物体从离开电场II开始,到平板速度最大时,所需要的时间。
如图所示,一辆质量M="3" kg的小车A静止在光滑的水平面上,小车上有一质量m="l" kg的光滑小球B,将一轻质弹簧压缩并锁定,此时弹簧的弹性势能为Ep=6J,小球与小车右壁距离为L=0.4m,解除锁定,小球脱离弹簧后与小车右壁的油灰阻挡层碰撞并被粘住,求: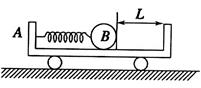
①小球脱离弹簧时的速度大小;
②在整个过程中,小车移动的距离。