如图,已知抛物线y=ax2+bx+c(a>0,c<0)交x轴于点A,B,交y轴于点C,设过点A,B,C三点的圆与y轴的另一个交点为D.
(1)如图1,已知点A,B,C的坐标分别为(-2,0),(8,0),(0,-4);
①求此抛物线的函数解析式;
②若点M为抛物线上的一动点,且位于第四象限,求△BDM面积的最大值;
(2)如图2,若a=1,c=-4,求证:无论b取何值,点D的坐标均不改变.
如图,已知某小区的两幢10层住宅楼间的距离为AC="30" m,由地面向上依次为第1层、第2层、…、第10层,每层高度为3 m.假设某一时刻甲楼在乙楼侧面的影长EC=h,太阳光线与水平线的夹角为α .
用含α的式子表示h(不必指出α的取值范围);
当α=30°时,甲楼楼顶B点的影子落在乙楼的第几层?若α每小时增加15°,从此时起几小时后甲楼的影子刚好不影响乙楼采光?(
 取1.73)
取1.73)
在下图中,每个正方形由边长为1 的小正方形组成: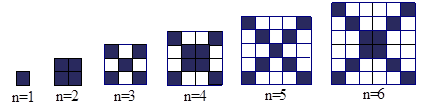
观察图形,请填写下列表格:
| 正方形边长 |
1 |
3 |
5 |
7 |
… |
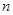 (奇数) (奇数) |
| 黑色小正方形个数 |
… |
| 正方形边长 |
2 |
4 |
6 |
8 |
… |
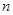 (偶数) (偶数) |
| 黑色小正方形个数 |
… |
在边长为
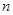 (n≥1)的正方形中,设黑色小正方形的个数为
(n≥1)的正方形中,设黑色小正方形的个数为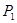 ,白色小正方形的个数为
,白色小正方形的个数为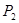 ,问是否存在偶数
,问是否存在偶数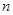 ,使
,使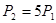 ?若存在,请写出
?若存在,请写出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
将图⑴中的矩形ABCD沿对角线 剪开,再把△ABC沿着AD方向平移,得到图⑵中的△A′BC′,除△ADC与△C′BA′全等外,你还可以指出哪几对全等的三角形(不能添加辅助线和字母)?请选择其中一对加以证明.
剪开,再把△ABC沿着AD方向平移,得到图⑵中的△A′BC′,除△ADC与△C′BA′全等外,你还可以指出哪几对全等的三角形(不能添加辅助线和字母)?请选择其中一对加以证明.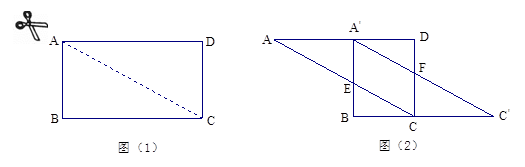
有四张背面相同的纸牌A,B,C,D,其正面分别画有四个不同的几何图形(如图).小华将这4张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸出一张.用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A,B,C,D表示);
求摸出两张牌面图形都是中心对称图形的纸牌的概率.
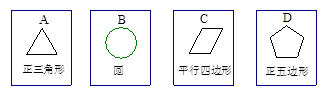
先化简,再求值: ,其中x=-4.
,其中x=-4.