在Rt△ABC中，∠ACB=90°，AC=2，BC=4．点D是线段BC上的一个动点．点D与点B、C不重合，过点D作DE⊥BC交AB于点E，将△ABC沿着直线DE翻折，使点B落在直线BC上的F点．
（1）设∠BAC=α（如图①），求∠AEF的大小；（用含α的代数式表示）
（2）当点F与点C重合时（如图②），求线段DE的长度；
（3）设BD=x，△EDF与△ABC重叠部分的面积为S，试求出S与x之间函数关系式，并写出自变量x的取值范围．
选择适当的方法解下列一元二次方程：
（1）
（2）
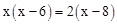
（1）计算：
；
（2）先化简，再求值：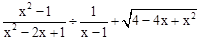
，其中x=3.
数学课上，探讨角平分线的作法时，李老师用直尺和圆规作角平分线，方法如下：
小聪只带了直角三角板，他发现利用三角板也可以作角平分线，方法如下：
步骤：①利用三角板上的刻度，在OA和OB上分别截取OM、ON，使OM＝ON．
②分别过M、N作OM、ON的垂线，交于点P．
③作射线OP．则OP为∠AOB的平分线．
小颖的身边只有刻度尺，经过尝试，她发现利用刻度尺也可以作角平分线．
根据以上情境，解决下列问题：
(1)李老师用尺规作角平分线时，用到的三角形全等的判定方法是_______．
(2)小聪的作法正确吗？请说明理由．
(3)请你帮小颖设计用刻度尺作角平分线的方法．（要求：作出图形，写出作图步骤，不予证明）
如图1，在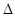
ABC中，AB=AC，点D是BC的中点，点E在AD上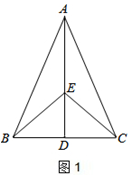
⑴求证：BE=CE；
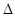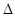⑵如图2，若BE的延长线交AC于点F，且BF⊥AC,垂足为F，∠BAC=45°，原题设其它条件不变. 求证：AEF≌BCF.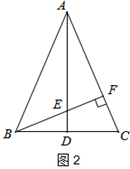
（8分)如图，在长方形ABCD中，将△ABC沿AC对折至△AEC位置，CE与AD交于点F．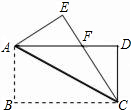
(1)试说明：AF＝FC；
(2)如果AB＝3，BC＝4，求AF的长．