如图（a）所示，水平放置的平行金属板AB间的距离d=0.1m，板长L=0.3m，在金属板的左端竖直放置一带有小孔的挡板，小孔恰好位于AB板的正中间，距金属板右端x=0.5m处竖直放置一足够大的荧光屏，现在AB板间加如图（b）所示的方波形电压，已知U0=1.0×102V，在挡板的左侧，有大量带正电的相同粒子以平行于金属板方向的速度持续射向挡板，粒子的质量m=1.0×10-7kg，电荷量q=1.0×10-2C，速度大小均为v0=1.0×104m/s，带电粒子的重力不计，则：
（1）求电子在电场中的运动时间；
（2）求在t=0时刻进入的粒子飞出电场时的侧移量；
（3）求各个时刻进入的粒子，离开电场时的速度的大小和方向；
（4）若撤去挡板，求荧光屏上出现的光带长度。
按照我国整个月球探测活动的计划，在第一步“绕月”工程圆满完成各项目标和科学探测任务后，将开展第二步“落月”工程。如图所示 假设月球半径为R，月球表面的重力加速度为g0，飞船沿距月球表面高度为3R的圆形轨道I上运动，当运动到轨道 上的A点时，点火变轨进人椭圆轨道II，在到达轨道的近月点B时再次点火变轨，进入近月轨道III绕月球做圆周运动。求：
（1）飞船在轨道I上的运行速率；
（2）飞船在轨道III上绕月球运动一周所需的时间？
如图甲所示，波源S从平衡位置y＝0处开始竖直向上振动（y轴的正方向），振动周期为T＝0.01 s，产生的简谐波向左、右两个方向传播，波速均为v＝80 m/s.经过一段时间后，P、Q两点开始振动，已知距离SP＝1.2 m，SQ＝2.6 m
a.求此波的频率和波长；
b.若以Q点开始振动的时刻作为计时的零点，试在图乙中分别画出P、Q两点的振动图象．
如图所示，带电平行金属板PQ和MN之间的距离为d；两金属板之间有垂直纸面向里的匀强磁场，磁感应强度大小为B。如图建立坐标系，x轴平行于金属板，与金属板中心线重合，y轴垂直于金属板。区域I的左边界在y轴，右边界与区域II的左边界重合，且与y轴平行；区域II的左、右边界平行。在区域I和区域II内分别存在匀强磁场，磁感应强度大小均为B，区域I内的磁场垂直于Oxy平面向外，区域II内的磁场垂直于Oxy平面向里。一电子沿着x轴正向以速度v0射入平行板之间，在平行板间恰好沿着x轴正向做直线运动，并先后通过区域I和II。已知电子电量为e，质量为m，区域I和区域II沿x轴方向宽度均为
。不计电子重力。
（1）求两金属板之间电势差U；
（2）求电子从区域II右边界射出时，射出点的纵坐标y；
（3）撤除区域I中的磁场而在其中加上沿x轴正向的匀强电场，使得该电子刚好不能从区域II的右边界飞出。求电子两次经过y轴的时间间隔t。
某兴趣小组对一辆自制遥控小车的性能进行研究。他们让这辆小车在水平的直轨道上由静止开始运动，并将小车运动的全过程记录下来，通过处理转化为v—t图象，如图所示（除2s—10s时间段图象为曲线外，其余时间段图象均为直线）。已知在小车运动的过程中，2s—14s时间段内小车的功率保持不变，在14s末停止遥控而让小车自由滑行，小车的质量为1.0kg，可认为在整个运动过程中小车所受到的阻力大小不变。求：
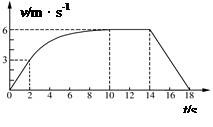
（1）小车所受到的阻力大小；
（2）小车匀速行驶阶段的功率；
（3）小车在加速运动过程中位移的大小。
如图所示，在以坐标原点O为圆心、半径为R的半圆形区域内，有相互垂直的匀强电场和匀强磁场，磁感应强度为B，磁场方向垂直于xOy平面向里．一带正电的粒子（不计重力）从O点沿y轴正方向以某一速度射入，带电粒子恰好做匀速直线运动，经t0时间从P点射出．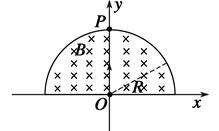
（1）求电场强度的大小和方向．
（2）若仅撤去磁场，带电粒子仍从O点以相同的速度射入，经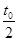
时间恰好从半圆形区域的边界射出．求粒子运动加速度的大小．
（3）若仅撤去电场，带电粒子仍从O点射入，但速度为原来的4倍，求粒子在磁场中运动的时间．