【情境阅读】
在图1中,点A在边OB上,点D在边OC上,且AD∥BC﹒将这样的图形定义为“A型”﹒将△OAD绕着点O旋转α°(0<α<90)得到新的图形(如图2),将图2中的四边形A′B′C′D′称为“准梯形”,A′D′称为上底,B′C′称为下底﹒
【新知学习】
(1)若情境阅读中的△OBC是等腰直角三角形,OB=OC,∠BOC=90°,其余条件不变﹒
①请说明图2中的△O′A′B′≌△O′D′C′﹒
②在图1中,S四边形ABCD=S△OBC﹣S△OAD,请探索图2中的S四边形A′B′C′D′与图1中的S四边形ABCD的大小关系﹒
【变式探究】
(2)如图3,四边形ABCD是由有一个角是60°的“A型”通过旋转变换得到的“准梯形”,AD是上底,BC是下底,且AB=5,BC=8,CD=5,DA=2﹒求这个“准梯形”的面积.
【迁移拓展】
(3)如图4是由具有公共直角顶点的“A型”绕着直角定点旋转α°(0<α<90)得到的“准梯形”,斜边AD为上底,斜边BC为下底,且AB=3,BC=4 ,CD=6,AD=3
,CD=6,AD=3 .求这个“准梯形”的面积.
.求这个“准梯形”的面积.
如图,AD是ΔABC的外角∠CAE的平分线,∠B=30°,∠DAE=55°,试求:(1)∠BAC的度数; (2)∠ACB的度数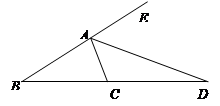
学校组织同学们参加劳动实践.如图,是要做的一个零件形状.按规定,图中的∠A应等于90°,∠B和∠C分别是28°和20°.检验人员度量出王刚同学所做零件中的∠BDC=140°,请你应用所学的数学知识确定这个零件是否合格,并说明你的理由.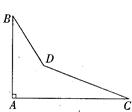
有一句谚语说:“捡了芝麻,丢了西瓜。”意思是说有些人办事只抓一些无关紧要的小事,却忽略了具有重大意义的大事。据测算,5万粒芝麻才200克,你能换算出1粒芝麻有多少克吗?可别“占小便宜吃大亏”噢!(把你的结果用科学记数法表示)
计算与化简
(1) 计算:
(2) 计算:
(3)计算:
(4)计算: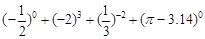
(5)先化简,再求值: ,其中
,其中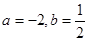
2012年7月6日在湖南省展览馆举行了长沙动漫展,很多中学生也对动漫产生了浓厚
的兴趣,某动漫公司决定在假期举行一次中学生动漫画展,经调查发现,活动最低票价
为10元,如果以10元票价开放,平均每天有100个学生来观看,若票价每提高1元,
则相应减少10个参观者。
(1)写出平均每天观看动漫展的学生人数y(单位:人)与票价x (x为整数,单位:元)之间的关系;
(2)如果要使每天总收入为910元,票价应定为多少元?