如图1,已知:抛物线y=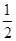 x2+bx+c与x轴交于A,B两点,与y轴交于点C,经过B,C两点的直线是y=
x2+bx+c与x轴交于A,B两点,与y轴交于点C,经过B,C两点的直线是y=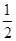 x-2,连结AC.
x-2,连结AC.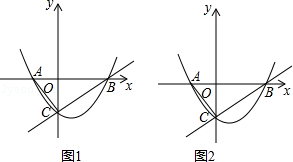
(1)求出抛物线的函数关系式;
(2)若△ABC内部能否截出面积最大的矩形DEFC(顶点D、E、F、G在△ABC各边上)?若能,求出在AB边上的矩形顶点的坐标;若不能,请说明理由.
(3)点P(t,0)是x轴上一动点,P、Q两点关于直线BC成轴对称,PQ交BC于点M,作QH⊥x轴于点H.连结OQ,是否存在t的值,使△OQH与△APM相似?若存在,求出t的值;若不存在,说明理由.
如图,四边形ABCD内接于⊙O,AD∥BC,P为BD上一点,∠APB=∠BAD.
(1)AB=CD;
(2)DP•BD=AD•BC;
(3) .
.
如图1,AB为⊙O的直径,点P是直径AB上任意一点,过点P作弦CD⊥AB,垂足为P,过点B的直线与线段AD的延长线交于点F,且∠F=∠ABC.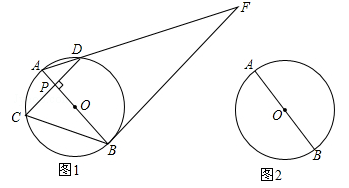
(1)若CD= ,BP=4,求⊙O的半径;
,BP=4,求⊙O的半径;
(2)求证:直线BF是⊙O的切线;
(3)当点P与点O重合时,过点A作⊙O的切线交线段BC的延长线于点E,在其它条件不变的情况下,判断四边形AEBF是什么特殊的四边形?请在图2中补全图象并证明你的结论.
(·辽宁辽阳)如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,E,DG⊥AC于点G,交AB的延长线于点F.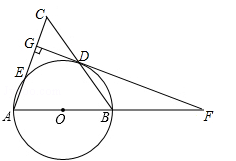
(1)求证:直线FG是⊙O的切线;
(2)若AC=10,cosA=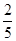 ,求CG的长.
,求CG的长.
如图,四边形ABCD为矩形,E为BC边中点,连接AE,以AD为直径的⊙O交AE于点F,连接CF.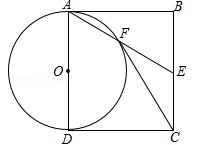
(1)求证:CF与⊙O相切;
(2)若AD=2,F为AE的中点,求AB的长.
如图,在△ABC中,以AB为直径的⊙O交AC于点D,过点D作DE⊥BC于点E,且∠BDE=∠A.
(1)判断DE与⊙O的位置关系,并说明理由;
(2)若AC=16,tanA=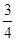 ,求⊙O的半径.
,求⊙O的半径.