操作:将一个边长为1的等边三角形(如图1)的每一边三等分,以居中那条线段为底边向外作等边三角形,并去掉所作的等边三角形的一条边,得到一个六角星(如图2),称为第一次分形.接着对每个等边三角形凸出的部分继续上述过程,即在每条边三等分后的中段向外画等边三角形,得到一个新的图形(如图3),称为第二次分形.不断重复这样的过程,就能得到雪花曲线.
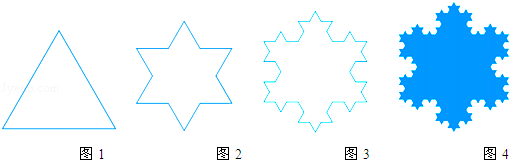
问题:
(1)从图形的对称性观察,图4是 图形(轴对称或中心对称图形)
(2)图2的周长为 ;
(3)试猜想第n次分形后所得图形的周长为 .
将二次函数 的图象先向右平移一个单位,再沿 轴翻折到第一象限,然后向右平移一个单位,再沿 轴翻折到第二象限 以此类推,如果把向右平移一个单位再沿坐标轴翻折一次记作 次变换,那么二次函数 的图象经过 次变换后,得到图象的函数解析式为_____.
关于抛物线 ,给出下列结论:①当 时,抛物线与直线 没有交点;②若抛物线与 轴有两个交点,则其中一定有一个交点在点 与 之间;③若抛物线的顶点在点 围成的三角形区域内(包括边界),则 .其中正确结论的序号是_____.
抛物线 绕其顶点旋转 所得抛物线的解析式为_____.
已知函数 在 上的最大值是 ,最小值是 ,则 的取值范围为_____.
已知二次函数 的图象与 轴的两个不同的交点到原点的距离之和不超过 ,则 的取值范围是_____.