某公司生产的某种时令商品每件成本为20元，经过市场调研发现，-优题课

题文

某公司生产的某种时令商品每件成本为20 元，经过市场调研发现，这种商品在未来40天内的日销售量Q（件）与时间t（天）的关系如下表：

时间（天）	1	3	6	10	36	…
日销售量（件）	94	90	84	76	24	…

未来40天内，前20天每天的价格y₁（元/件）与时间t（天）的函数关系式为：y₁=t+25（1≤t≤20且t为整数）；后20天每天的价格y₂（元/件）与时间t（天）的函数关系式为：y₂=﹣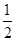t+40（21≤t≤40且t为整数）．
（1）求Q（件）与时间t（天）的函数关系式；
（2）请预测未来40天中哪一天的销售利润最大，最大日销售利润是多少？
（3）在实际销售的前20天中该公司决定每销售一件商品就捐赠a元利润（a＜4）给希望工程，公司通过销售记录发现，前20 天中，每天扣除捐赠后的日销售利润随时间t的增大而增大，求a的取值范围．

科目数学题型解答题难度较难

知识点：二次函数在给定区间上的最值

登录免费查看答案和解析

相关试题

如图， $ΔABC$ 中， $D$ 为 $BC$ 边上的一点， $AD = AC$ ，以线段 $AD$ 为边作 $ΔADE$ ，使得 $AE = AB$ ， $∠ BAE = ∠ CAD$ ．求证： $DE = CB$ ．

解不等式组： $\{\begin{matrix} x + 1 < 2, \\ 2 (1 - x) ⩽ 6 \cdot \end{matrix}$ 并把解集在数轴上表示出来．

如图， $ΔABC$ 中， $AB = AC$ ， $⊙ O$ 是 $ΔABC$ 的外接圆， $BO$ 的延长线交边 $AC$ 于点 $D$ ．

[小题1]求证： $∠ BAC = 2 ∠ ABD$ ；

[小题2]当 $ΔBCD$ 是等腰三角形时，求 $∠ BCD$ 的大小；

[小题3]当 $AD = 2$ ， $CD = 3$ 时，求边 $BC$ 的长．

在平面直角坐标系 $xOy$ 中，直线 $y = - \frac{1}{2} x + 5$ 与 $x$ 轴、 $y$ 轴分别交于点 $A$ 、 $B$ （如图）．抛物线 $y = a x^{2} + bx (a \neq 0)$ 经过点 $A$ ．

[小题1]求线段 $AB$ 的长；

[小题2]如果抛物线 $y = a x^{2} + bx$ 经过线段 $AB$ 上的另一点 $C$ ，且 $BC = \sqrt{5}$ ，求这条抛物线的表达式；

[小题3]如果抛物线 $y = a x^{2} + bx$ 的顶点 $D$ 位于 $ΔAOB$ 内，求 $a$ 的取值范围．

已知：如图，在菱形 $ABCD$ 中，点 $E$ 、 $F$ 分别在边 $BC$ 、 $CD$ 上， $BE = FD$ ， $AF$ 的延长线交 $BC$ 的延长线于点 $H$ ， $AE$ 的延长线交 $DC$ 的延长线于点 $G$ ．

[小题1]求证： $ΔAFD ∽ ΔGAD$ ；

[小题2]如果 $D F^{2} = CF \cdot CD$ ，求证： $BE = CH$ ．

试卷网试题网古诗词网作文网范文网

Copyright ©2020-2025 优题课 youtike.com 版权所有

粤ICP备20024846号