【提出问题】如图1,小东将一张AD为12,宽AB为4的长方形纸片按如下方式进行折叠:在纸片的一边BC上分别取点P、Q,使得BP=CQ,连结AP、DQ,将△ABP、△DCQ分别沿AP、DQ折叠得△APM,△DQN,连结MN.小东发现线段MN的位置和长度随着点P、Q的位置发生改变.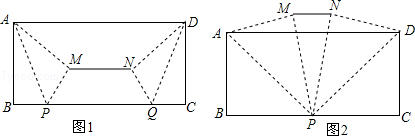
【规律探索】
(1)请在图1中过点M,N分别画ME⊥BC于点E,NF⊥BC于点F.
求证:①ME=NF;②MN∥BC.
【解决问题】
(2)如图1,若BP=3,求线段MN的长;
(3)如图2,当点P与点Q重合时,求MN的长.
如图,在平面直角坐标系中,已知点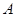 坐标为(2,4),直线x=2与
坐标为(2,4),直线x=2与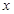 轴相交于点
轴相交于点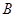 ,连结
,连结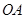 ,抛物线y=x
,抛物线y=x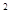
 从点
从点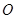 沿
沿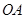 方向平移,与直线x=2交于点
方向平移,与直线x=2交于点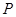 ,顶点
,顶点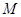 到
到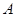 点时停止移动.
点时停止移动.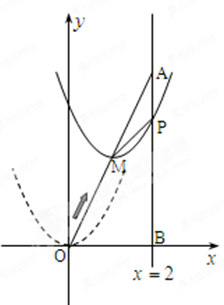
(1)求线段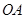 所在直线的函数解析式;
所在直线的函数解析式;
(2)设抛物线顶点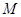 的横坐标为
的横坐标为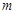 ,
,
①用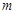 的代数式表示点
的代数式表示点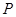 的坐标;
的坐标;
②当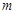 为何值时,线段
为何值时,线段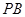 最短;
最短;
(3)当线段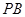 最短时,相应的抛物线上是否存在点
最短时,相应的抛物线上是否存在点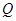 ,使△
,使△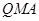 的面积与△
的面积与△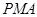 的面积相等,若存在,请求出点
的面积相等,若存在,请求出点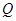 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
某跳水运动员进行10m跳台跳水的训练时,身体(看成一点)在空中的运动路线是如图所示坐标系下经过原点O的一条抛物线(图中标出的数据为己知条件).在跳某个规定动作时,正确情况下,该运动员在空中的最高处距水面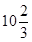 m,入水处与池边的距离为4m, 同时,运动员在距水面高度为5m以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.
m,入水处与池边的距离为4m, 同时,运动员在距水面高度为5m以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.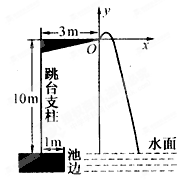
(l)求这条抛物线的解析式;
(2)在某次试跳中,测得运动员在空中的运动路线是(1)中的抛物线,且运动员在空中调整好入水姿势时,距池边的水平距离为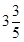 ,问:此次跳水会不会失误?通过计算说明理由.
,问:此次跳水会不会失误?通过计算说明理由.
跳绳时,绳甩到最高处时的形状是抛物线.正在甩绳的甲.乙两名同学拿绳的手间距AB为6米,到地面的距离AO和BD均为0.9米,身高为1.4米的小丽站在距点O的水平距离为1米的点F处,绳子甩到最高处时刚好通过她的头顶点E.以点O为原点建立如图所示的平面直角坐标系, 设此抛物线的解析式为y=ax2+bx+0.9.
(1)求该抛物线的解析式 .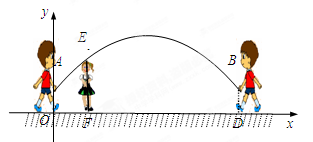
(2)如果小华站在OD之间,且离点O的距离为3米,当绳子甩到最高处时刚好通过他的头顶,小华的身高为;
(3)如果身高为1.4米的小丽站在OD之间,且离点O的距离为t米, 绳子甩到最高处时超过她的头顶,请结合图像,写出t的取值范围.
如图所示,MN表示某饮水工程的一段设计路线,从M到N的走向为南偏东30°,在M的南偏东60°的方向上有一点A,以点A为圆心.以500m为半径的圆形区域为居民区,取MN上另一点B,测得BA的方向为南偏东75°,已知MB=400m.通过计算回答,如果不改变方向,输水路线是否会穿过该居民区?(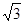 ≈1.73)
≈1.73)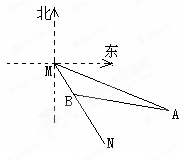
宁波元康水果市场某批发商经销一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,若每千克涨价一元,日销售量将减少20千克.
(1)现要保证每天盈利6000元,同时又要让顾客得到实惠,那么每千克应涨价多少元?
(2)若该批发商单纯从经济角度看,那么每千克应涨价多少元,能使商场获利最多.