(本小题满分12分)数列 的前
的前 项和
项和 ,
,
(1)求数列 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列 的前
的前 项和
项和 .
.
已知x、y满足 ,求
,求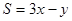 的最值。
的最值。
实数m取什么值时,复数z=(m2-5m+6)+(m2-3m) 是
是
(1)实数?(2)虚数?(3)纯虚数?
把下列方程化为直角坐标方程(并说明对应的曲线):
① ②
②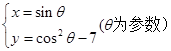
在直角坐标系xOy中,直线l的方程为x-y+4=0,曲线C的参数方程为 .
.
(Ⅰ)已知在极坐标(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为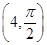 ,判断点P与直线l的位置关系;
,判断点P与直线l的位置关系;
(Ⅱ)设点Q是曲线C上的一个动点,求它到直线l的距离的最值;
(Ⅲ)请问是否存在直线 ,
, ∥l且
∥l且 与曲线C的交点A、B满足
与曲线C的交点A、B满足 ;
;
若存在请求出满足题意的所有直线方程,若不存在请说明理由。
在直角坐标系xoy中,直线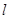 的参数方程为
的参数方程为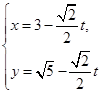 (t为参数)。在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数)。在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为 。
。
(Ⅰ)求圆C的直角坐标方程;
(Ⅱ)设圆C与直线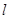 交于点A、B,若点P的坐标为
交于点A、B,若点P的坐标为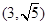 ,求|PA|+|PB|。
,求|PA|+|PB|。