（本小题满分12分）某校为了解高三年级不同性别的学生对取消艺术课的态度（支持或反对），进行了如下的调查研究．全年级共有1350人，男女生比例为8：7，现按分层抽样方法抽取若干名学生，每人被抽到的概率均为
，通过对被抽取学生的问卷调查，得到如下2x2列联表：
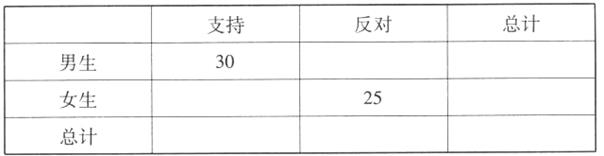
（1）完成列联表，并判断能否有99．9%的把握认为态度与性别有关？
（2）若某班有6名男生被抽到，其中2人支持，4人反对；有4名女生被抽到，其中2人支持，2人反对，现从这10人中随机抽取一男一女进一步调查原因．求其中恰有一人支持一人反对的概率．
（本小题满分10分）
甲、乙、丙三名射击运动员射中目标的概率分别为
，三人各射击一次，击中目标的次数记为
.
（1）求的分布列及
数学期望；
（2）在概率
(
=0，1，2，3)中, 若
的值最大, 求实数
的取值范围.
（本小题满分10分）
已知动圆
过点
且与直线
相切.
（1）求点的轨迹
的方程；
（2）过点
作一条直线交轨迹于
两点，轨迹在两点处的切线相交于点
，
为线段
的中点，求证：
轴.
D.选修4—5：不等式选讲
(本小题满分10分)
求函数
的最大值．
C．选修4—4：坐标系与参数方程
(本小题满分10分)
在极坐标系中，圆
的方程为
，以极点为坐标原点，极轴为
轴的正半轴建立平面直角坐标系，直线
的参数方程为
（
为参数），判断直线和圆的位置关系．
B．选修4—2：矩阵与变换
(本小题满分10分)[
已知矩阵
的一个特征值为3，求另一个特征值及其对应的一个特征向量.