(·湖南株洲)已知AB是圆O的切线,切点为B,直线AO交圆O于C、D两点,CD=2,∠DAB=30°,动点P在直线AB上运动,PC交圆O于另一点Q,
(1)当点P,运动到Q、C两点重合时(如图1),求AP的长。
(2)点运动过程中,有几个位置(几种情况)使△CQD的面积为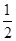 ?( 直接写出答案)
?( 直接写出答案)
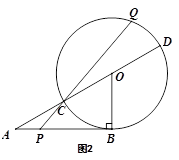
(3)当使△CQD的面积为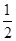 ,且Q位于以CD为直径的的上半圆上,CQ>QD时(如图2),求AP的长。
,且Q位于以CD为直径的的上半圆上,CQ>QD时(如图2),求AP的长。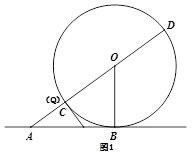
(·湖南长沙)如图,在直角坐标系中,⊙M经过原点O(0,0),点A(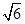 ,0)与点B(0,-
,0)与点B(0,-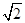 ),点D在劣弧OA上,连接BD交x轴于点C,且∠COD=∠CBO。
),点D在劣弧OA上,连接BD交x轴于点C,且∠COD=∠CBO。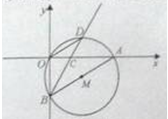
(1)求⊙M的半径;
(2)求证:BD平分∠ABO;
(3)在线段BD的延长线上找一点E,使得直线AE恰为⊙M的切线,求此时点E的坐标。
(·湖南常德)已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF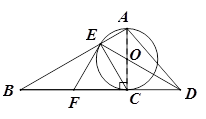
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为3,∠EAC=60°,求AD的长。
(·湖北孝感)如图,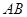 为⊙O的直径,
为⊙O的直径,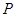 是
是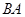 延长线上一点,
延长线上一点,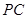 切⊙O于点
切⊙O于点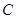 ,
,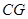 是⊙O的弦,
是⊙O的弦,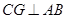 ,垂足为
,垂足为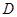 .
.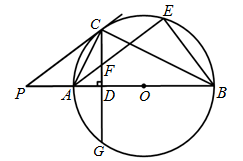
(1)求证: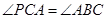 ;
;
(2)过点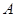 作
作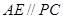 交⊙O于点
交⊙O于点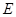 ,交
,交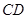 于点
于点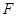 ,连接
,连接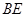 .若
.若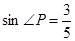 ,
,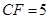 ,求
,求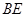 的长.
的长.
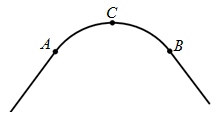
(·湖北孝感) 如图,一条公路的转弯处是一段圆弧(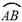 ).
).
(1)用直尺和圆规作出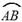 所在圆的圆心
所在圆的圆心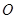 ;(要求保留作图痕迹,不写作法)
;(要求保留作图痕迹,不写作法)
(2)若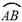 的中点
的中点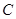 到弦
到弦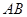 的距离为
的距离为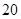 m,
m,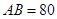 m,求
m,求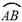 所在圆的半径.
所在圆的半径.