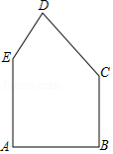
已知:在△ABC中,AB=AC,∠BAC=90°,点D是BC的中点,点P是BC边上的一个动点,连接AP.直线BE垂直于直线AP,交AP于点E,直线CF垂直于直线AP,交AP于点F.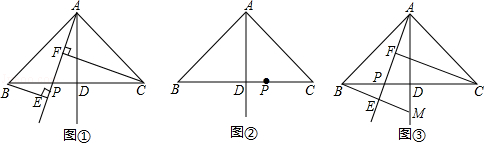
(1)当点P在BD上时(如图①),求证:CF=BE+EF;
(2)当点P在DC上时(如图②),CF=BE+EF还成立吗?若不成立,请画出图形,并直接写出CF、BE、EF之间的关系(不需要证明).
(3)若直线BE的延长线交直线AD于点M(如图③),找出图中与CP相等的线段,并加以证明.
先化简,再求值: ,其中 .
计算: .
如图,矩形 中, , ,点 , 分别在边 , 上,点 , 分别在边 , 上, , 交于点 ,记 .
(1)若 的值为1,当 时,求 的值.
(2)若 的值为 ,求 的最大值和最小值.
(3)若 的值为3,当点 是矩形的顶点, , 时,求 的值.
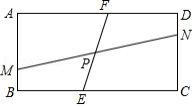
如图1是实验室中的一种摆动装置, 在地面上,支架 是底边为 的等腰直角三角形,摆动臂 可绕点 旋转,摆动臂 可绕点 旋转, , .
(1)在旋转过程中,
①当 , , 三点在同一直线上时,求 的长.
②当 , , 三点为同一直角三角形的顶点时,求 的长.
(2)若摆动臂 顺时针旋转 ,点 的位置由 外的点 转到其内的点 处,连结 ,如图2,此时 , ,求 的长.
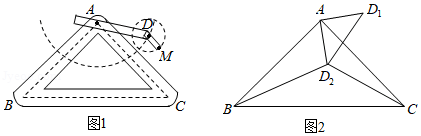
有一块形状如图的五边形余料 , , , , , ,要在这块余料中截取一块矩形材料,其中一条边在 上,并使所截矩形材料的面积尽可能大.
(1)若所截矩形材料的一条边是 或 ,求矩形材料的面积.
(2)能否截出比(1)中更大面积的矩形材料?如果能,求出这些矩形材料面积的最大值;如果不能,说明理由.