在市政府实施市容市貌工程期间,某中学在教学楼前铺设小广场地面.其图案设计如图1,正方形小广场地面的边长是40m,中心建一直径为20m的圆形花坛,四角各留一个边长为10m的小正方形花坛,种植高大树木.图中其余部分铺设广场砖.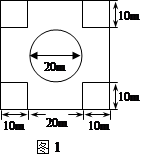
(1)请同学们帮助计算铺设广场砖部分的面积 (
( 取3);
取3);
(2)某施工队承包铺设广场砖的任务,计划在一定时间内完成,按计划工作一天后,由于改进了铺设工艺,每天比原计划多铺60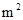 ,结果提前3天完成了任务,原计划每天铺设多少
,结果提前3天完成了任务,原计划每天铺设多少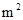 ?
?
(3)如图2表示广场中心圆形花坛的平面图,准备在圆形花坛内种植6种不同颜色的花卉,为了美观,要使同色花卉集中在一起,并且各花卉的种植面积相等.请你帮助设计一种方案,画在图2上.(不必说明方案,不写作法,保留作图痕迹)
如图,在△ABC中,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB.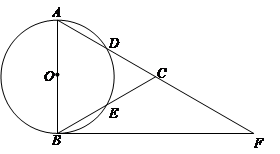
(1)求证:直线BF是⊙O的切线;
(2)若点D,点E分别是弧AB的三等分点,当AD=5时,求BF的长.
已知点P(2,2)在反比例函数 的图象上.
的图象上.
(1)当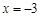 时,求
时,求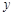 的值;
的值;
(2)当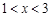 时,求
时,求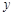 的取值范围.
的取值范围.
为更好地宣传“开车不喝酒,喝酒不开车”的驾车理念,某市一家报社设计了如下的调查问卷(单选).在随机调查了本市全部8000名司机中的部分司机后,统计整理并制作了如下的统计图:

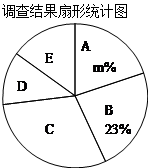
根据以上信息解答下列问题:
(1)补全条形统计图,并计算扇形统计图中m=________;
(2)该市支持选项B的司机大约有多少人?
(3)若要从该市支持选项B的司机中随机选择100名,给他们发放“请勿酒驾”的提醒标志,则支持该选项的司机王明被选中的概率是多少?
求代数式的值: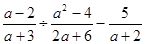 ,其中a=
,其中a= .
.