已知菱形纸片ABCD的边长为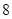 ,∠A=60°,E为
,∠A=60°,E为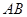 边上的点,过点E作EF∥BD交AD于点F.将菱形先沿EF按图1所示方式折叠,点A落在点
边上的点,过点E作EF∥BD交AD于点F.将菱形先沿EF按图1所示方式折叠,点A落在点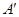 处,过点
处,过点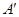 作GH∥BD分别交线段BC、DC于点G、H,再将菱形沿GH按图1所示方式折叠,点C落在点
作GH∥BD分别交线段BC、DC于点G、H,再将菱形沿GH按图1所示方式折叠,点C落在点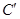 处,
处,  与
与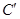 H分别交
H分别交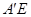 与
与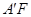 于点M、N.若点
于点M、N.若点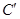 在△
在△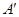 EF的内部或边上,此时我们称四边形
EF的内部或边上,此时我们称四边形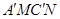 (即图中阴影部分)为“重叠四边形”.
(即图中阴影部分)为“重叠四边形”.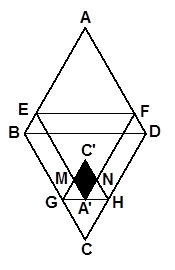

若把菱形纸片ABCD放在菱形网格中(图中每个小三角形都是边长为1的等边三角形),点A、B、C、D、E恰好落在网格图中的格点上.如图2所示,请直接写出此时重叠四边形
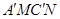 的面积;
的面积;实验探究:设AE的长为
 ,若重叠四边形
,若重叠四边形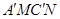 存在.试用含
存在.试用含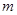 的代数式表示重叠四边形
的代数式表示重叠四边形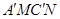 的面积,并写出
的面积,并写出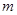 的取值范围(直接写出结果,备用图供实验,探究使用).
的取值范围(直接写出结果,备用图供实验,探究使用).
为迎接“六一”儿童节的到来,某校学生参加献爱心捐款活动,随机抽取该校部分学生的捐款数进行统计分析,相应数据的统计图如下:
(1)该校本的容量是,样本中捐款15元的学生有人;
(2)若该校一共有500名学生,据此样本估计该校学生的捐款总数.
解不等式组和分式方程:
(1)解不等式组:
(2)解分式方程:
计算与化简:
(1)计算:
(2)化简: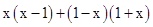
观察下列关于自然数的等式:
32﹣4×12=5①
52﹣4×22=9②
72﹣4×32=13③
…
根据上述规律解决下列问题:
(1)完成第四个等式:92﹣4× _________ 2= _________ ;
(2)写出你猜想的第n个等式(用含n的式子表示),并验证其正确性.
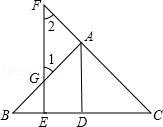
如图所示,已知AD⊥BC于点D,FE⊥BC于点E,交AB于点G,交CA的延长线于点F,且∠1=∠F.问:AD平分∠BAC吗?并说明理由.