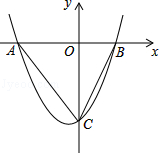
如图,抛物线y=ax2+bx﹣5(a≠0)与x轴交于点A(﹣5,0)和点B(3,0),与y轴交于点C.
(1)求该抛物线的解析式;
(2)若点E为x轴下方抛物线上的一动点,当S△ABE=S△ABC时,求点E的坐标;
(3)在(2)的条件下,抛物线上是否存在点P,使∠BAP=∠CAE?若存在,求出点P的横坐标;若不存在,请说明理由.
(本小题10分)
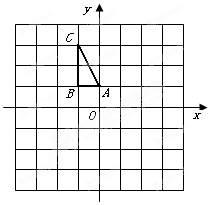
如图,在平面直角坐标系中, 的三个顶点的坐标分别为
的三个顶点的坐标分别为 .
.
(1)画出
 关于x轴对称的
关于x轴对称的 ,并写出点
,并写出点 的坐标.
的坐标.(2)画出
 绕原点
绕原点 顺时针方向旋转90°后得到的
顺时针方向旋转90°后得到的 ,并写出点
,并写出点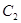 的坐标.
的坐标.(3)将
 平移得到
平移得到 ,使点
,使点 的对应点是
的对应点是 ,点
,点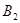 的对应点是
的对应点是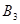 ,点
,点 的对应点是
的对应点是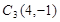 ,在坐标系中画出
,在坐标系中画出 ,并写出点
,并写出点 ,
, 的坐标.
的坐标.
(本小题8分)
如图,已知:点B、F、C、E在一条直线上,FB=CE,AC=DF.能否由上面的已知条件证明AB∥ED?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件,添加到已知条件中,使AB∥ED成立,并给出证明.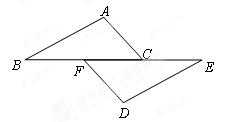
供选择的三个条件(请从其中选择一个):
①AB=ED;②BC=EF;③∠ACB=∠DFE.
(本小题10分)(1)解不等式:
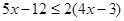
(2)解方程:
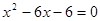
(本小题10分)(1)计算:
 ;
;(2)化简:

.在△ABC中,∠C=90°,AC=4cm,BC=5cm,点D在BC上,并且CD=3cm,现有两个动点P、Q分别从点A和点B同时出发,其中点P以1cm/s的速度,沿AC向终点C移动;点Q以1.25cm/s的速度沿BC向终点C移动.过点P作PE∥BC交AD于点E,连结EQ.设动点运动时间为x秒.(1)用含x的代数式表示AE、DE的长度;
(2)当点Q在线段BD(不包括点B、D)上移动时,设△EDQ的面积为
 ,求
,求 与
与 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围;
的取值范围;(3)当
 为何值时,△EDQ为直角三角形.
为何值时,△EDQ为直角三角形.