已知任意三角形的三边长，如何求三角形面积？

古希腊的几何学家海伦解决了这个问题，在他的著作《度量论》一书中给出了计算公式﹣﹣海伦公式 $S=\sqrt{p(p-a)(p-b)(p-c)}$（其中a，b，c是三角形的三边长， $p=\frac{a+b+c}{2}$，S为三角形的面积），并给出了证明

例如：在△ABC中，a＝3，b＝4，c＝5，那么它的面积可以这样计算：

∵a＝3，b＝4，c＝5

∴ $p=\frac{a+b+c}{2}=6$

∴ $S=\sqrt{p(p-a)(p-b)(p-c)}=\sqrt{6\times 3\times 2\times 1}=6$

事实上，对于已知三角形的三边长求三角形面积的问题，还可用我国南宋时期数学家秦九韶提出的秦九韶公式等方法解决．

根据上述材料，解答下列问题：

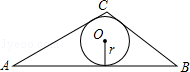
如图，在△ABC中，BC＝5，AC＝6，AB＝9

（1）用海伦公式求△ABC的面积；

（2）求△ABC的内切圆半径r．

科目 数学   题型 解答题   难度 中等

知识点： 二次根式的应用 三角形的内切圆与内心