一质量为2kg的物体在水平力F的作用下沿水平面做直线运动，一段时间后撤去F，其运动的v-t图象如图所示．g取10m/s2，求：
（1）物体与水平面间的动摩擦因数μ；
（2）水平推力F的大小．
(9分)一个物体质量m=50kg，以υo=2m/s的初速度沿斜面匀加速滑下，如图所示，斜面的倾角θ=37o，在t=5s的时间内滑下的位移为χ=60m。（g=10m/s2，sin37o=0.6，cos37o=0.8）
(1)对物体进行受力分析，画出受力图
(2)求物体的加速度的大小
(3)求物体受到的阻力的大小
(9分)如图所示，物体A的质量为10kg，放在水平地面上，物体A与地面间的动摩擦因素µ=0.2，如果用与水平面成37o的力F拉它，F=50N。若物体原来静止，则：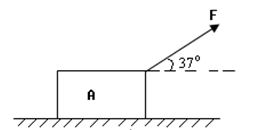
(1)物体2s末的速度是多少？
(2)物体2s 内的位移是多少？
（g=10m/s2，sin37o=0.6，cos37o=0.8）
(8分）一辆汽车以72km/h的速度在平直公路上行驶，现因故紧急刹车，已知汽车刹车过程中加速的的大小始终为5m/s2，求
（1）汽车刹车3s末的速度；
（2）汽车从开始刹车到6s末所通过的位移
如图所示，倾角为θ的斜面上只有AB段粗糙，其余部分都光滑，AB段长为3L．有若干个相同的小方块沿斜面靠在一起，但不粘接，总长为L．将它们由静止释放，释放时下端距A为2L．当下端运动到A下面距A为L/2时物块运动的速度达到最大．（单独研究一个小方块时可将其视为质点）
① 求物块与粗糙斜面的动摩擦因数；
② 求物块停止时的位置；
③ 要使所有物块都能通过B点，由静止释放时物块下端距A点至少要多远？
某电视台“快乐向前冲”节目中的场地设施如题图所示，AB为水平直轨道，上面安装有电动悬挂器，可以载人运动，水面上漂浮着一个半径为R，角速度为ω，铺有海绵垫的转盘，转盘的轴心离平台的水平距离为L，平台边缘与转盘平面的高度差为H．选手抓住悬挂器，可以在电动机带动下，从A点下方的平台边缘处沿水平方向做初速度为零，加速度为a的匀加速直线运动．选手必须作好判断，在合适的位置释放，才能顺利落在转盘上．设人的质量为m(不计身高大小)，人与转盘间的最大静摩擦力为μmg，重力加速度为g．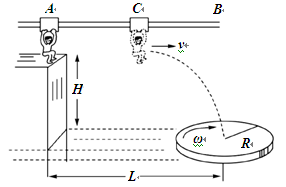
①假设选手落到转盘上瞬间相对转盘速度立即变为零，为保证他落在距圆心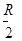
以内不会被甩出转盘，转盘的角速度ω应限制在什么范围?
②若已知H =" 5" m，L =" 8" m，a =" 2" m/s2，g =" 10" m/s2，且选手从某处C点释放能恰好落到转盘的圆心上，则他是从平台出发后经过多长时间释放悬挂器的?
③ 若电动悬挂器开动后，针对不同选手的动力与该选手重力关系皆为F = 0.6mg，悬挂器在轨道上运动时存在恒定的摩擦阻力，选手在运动到上面(2)中所述位置C点时，因恐惧没有释放悬挂器，但立即关闭了它的电动机，则按照(2)中数据计算悬挂器载着选手还能继续向右滑行多远的距离?