如图,在∠ABC中,AB = BC,D、E、F分别是BC、AC、AB边上的中点;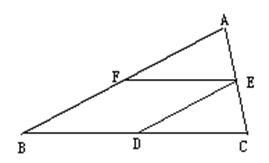
(1)求证:四边形BDEF是菱形;
(2)若AB = 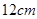 ,求菱形BDEF的周长.
,求菱形BDEF的周长.
如图,在平面直角坐标系中,以点M(0,3)为圆心、5为半径的圆与x轴交于点A、B(点A在点B的左侧),与y轴交于点C、D(点C在点D的上方),经过B、C两点的抛物线的顶点E在第二象限.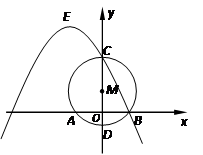
(1)求点A、B两点的坐标.
(2)当抛物线的对称轴与⊙M相切时, 求此时抛物线的解析式.
(3)连结AE、AC、CE,若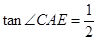 .
.
①求点E坐标;
②在直线BC上是否存在点P,使得以点B、M、P为顶点的三角形和△ACE相似?若存在,直接写出点P的坐标;若不存在,请说明理由.
如图所示,抛物线y=-x2+mx+n经过点A(1,0)和点C(4,0),与y轴交于点B。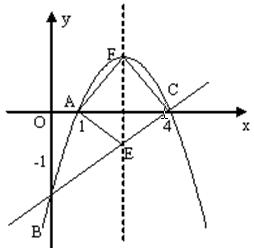
(1)求抛物线所对应的解析式。
(2)连接直线BC,抛物线的对称轴与BC交于点E,F为抛物线的顶点,求四边形AECF的面积。
已知在平面直角坐标系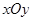 中,二次函数
中,二次函数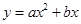 的图像经过点
的图像经过点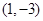 和点
和点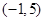 ;
;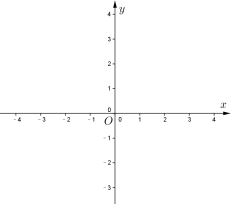
(1)求这个二次函数的解析式;
(2)将这个二次函数的图像向上平移,交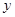 轴于点
轴于点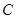 ,其纵坐标为
,其纵坐标为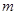 ,请用
,请用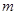 的代数式表示平移后函数图象顶点
的代数式表示平移后函数图象顶点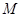 的坐标;
的坐标;
(3)在第(2)小题的条件下,如果点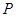 的坐标为
的坐标为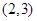 ,
,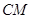 平分
平分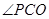 ,求
,求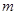 的值;
的值;
已知关于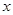 的一元二次方程
的一元二次方程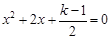 有实数根,
有实数根,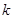 为正整数.
为正整数.
(1)求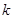 的值;
的值;
(2)当此方程有两个非零的整数根时,将关于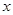 的二次函数
的二次函数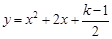 的图象向下平移9个单位,求平移后的图象的表达式;
的图象向下平移9个单位,求平移后的图象的表达式;
(3)在(2)的条件下,平移后的二次函数的图象与x轴交于点A,B(点A在点B左侧),直线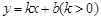 过点B,且与抛物线的另一个交点为C,直线BC上方的抛物线与线段BC组成新的图象,当此新图象的最小值大于-5时,求k的取值范围.
过点B,且与抛物线的另一个交点为C,直线BC上方的抛物线与线段BC组成新的图象,当此新图象的最小值大于-5时,求k的取值范围.
已知二次函数y=x2﹣4x+3.
(1)用配方法求其图象的顶点C的坐标,并描述该函数的函数值随自变量的增减而变化的情况;
(2)求函数图象与x轴的交点A,B的坐标,及△ABC的面积.