如图,已知二次函数 与 轴交于 、 两点(点 位于点 的左侧),与 轴交于点 ,已知 的面积是 6 .
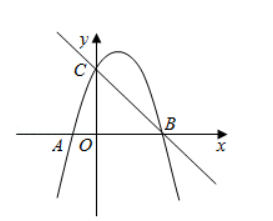
( 1 )求 的值;
( 2 )在抛物线上是否存在一点 ,使 .存在请求出 坐标,若不存在请说明理由.
(本题8分)先阅读下面文字,然后按要求解题.
例:1+2+3+…+100=?如果一个一个顺次相加显然太繁,我们仔细分析这100个连续自然数的规律和特点,可以发现运用加法的运算律,是可以大大简化计算,提高计算速度的.因为1+100=2+99=3+98=…=50+51=101,所以将所给算式中各加数经过交换、结合以后,可以很快求出结果.
解 1+2+3+…+100
=(1+100)+(2+99)+(3+98)+…+(50+51)
=101×=.
(1)在上面横线上补全例题解题过程;
(2)计算a+(a+b)+(a+2b)+(a+3b)+…+(a+99b).
(本题8分)小明去文具店购买2B铅笔,店主说:“如果多买一些,给你打8折”.小明测算了一下,如果买100支,比按原价购买可以便宜10元,求每支铅笔的原价是多少?
(本题7分)某公司的某种产品由一家商店代销,双方协议不论这种产品销售情况如何,该公司每月给商店m元代销费,同时商店每销售一件产品有5元提成,该商店一月份销售了n件,二月份比一月份多销售了20%.
(1)列式表示该商店二月份此种商品销售的件数;
(2)列式表示该商店二月份销售此种产品的收益;
(注:商店销售此种产品的收益=代销费+提成)
(3)假设代销费为每月200元,一月份销售了20件,求该商店二月份销售此种产品的收益.
(本题8分)已知关于x的方程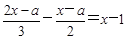 与方程3(x-2)=4x-5的解相同,求a的值.
与方程3(x-2)=4x-5的解相同,求a的值.
(本题6分)a,b为有理数,如果规定一种新的运算“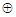 ”,定义:a
”,定义:a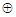 b=a2-ab+a-1,请根据“
b=a2-ab+a-1,请根据“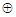 ”的定义计算下列各题:
”的定义计算下列各题:
例如:2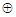 (-5)=
(-5)=
=4-(-10)+2-1=4+10+2-1=15
计算:(1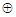 3)
3)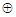 (-3)
(-3)