如图D,E分别是△ABC的AB,AC边上的点,且DE∥BC,AD∶AB=1∶4,
(1)证明:△ADE∽△ABC;
(2)当DE=2,求BC的长.
学校组织初一年级全体同学参加植树造林劳动.全体同学分成三队,第一队植树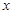 棵,第二队植的树比第一队植树的两倍少80棵,第三队植的树比第二队植树多了10
棵,第二队植的树比第一队植树的两倍少80棵,第三队植的树比第二队植树多了10 .
.
(1)求全体同学一共植树多少棵?(用含x的式子表示)
(2)若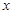 =100棵,求全体同学共植树多少棵?
=100棵,求全体同学共植树多少棵?
如图:化简:

李华用400元批发(购买)了8套儿童服装,全部卖出,如果每套以55元的价格为标准,超出的记作正数,不足的记作负数,记录如下:+2,-3,+2,+1,-2,-3,0,-2.问:李华在这次买卖中是盈利还是亏损,盈利或亏损多少元钱?
化简求值:
(1) ,其中
,其中 .
.
(2) ,其中
,其中 ,
,
(1)如图①所示,P是等边△ABC内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转60°得△BCQ,连接PQ.若PA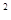 +PB
+PB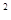 =PC
=PC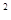 ,证明∠PQC=90°;
,证明∠PQC=90°;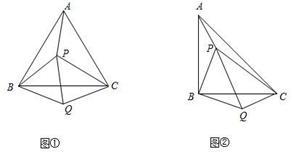
(2)如图②所示,P是等腰直角△ABC(∠ABC=90°)内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转90°得△BCQ,连接PQ.当PA、PB、PC满足什么条件时,∠PQC=90°?请说明.