如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x秒.
(1)当x为何值时,PQ∥BC;
(2)是否存在某一时刻,使△APQ∽△CQB,若存在,求出此时AP的长;若不存在,请说理由;
(3)当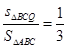 时,求
时,求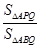 的值.
的值.
小明的妈妈在菜市场买回3斤萝卜、2斤排骨,准备做萝卜排骨汤.
妈妈:“今天买这两样菜共花了45元,上月买同重量的这两样菜只要36元”;
爸爸:“报纸上说了萝卜的单价上涨50%,排骨单价上涨20%”;
小明:“爸爸、妈妈,我想知道今天买的萝卜和排骨的单价分别是多少?”
请你通过列方程(组)求解这天萝卜、排骨的单价(单位:元/斤).
如图,等腰梯形ABCD放置在平面坐标系中,已知A(﹣2,0)、B(6,0)、D(0,3),反比例函数的图象经过点C.
(1)求点C的坐标和反比例函数的解析式;
(2)将等腰梯形ABCD向上平移2个单位后,问点B是否落在双曲线上?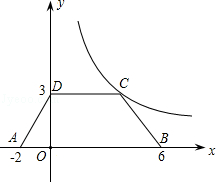
如图,已知两个菱形ABCD.CEFG,其中点A.C.F在同一直线上,连接BE、DG.
(1)在不添加辅助线时,写出其中的两对全等三角形;
(2)证明:BE=DG.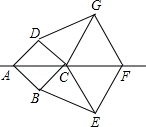
有两双大小、质地相同、仅有颜色不同的拖鞋(分左右脚,可用A1、A2表示一双,用B1、B2表示另一双)放置在卧室地板上.若从这四只拖鞋中随即取出两只,利用列表法(树形图或列表格)表示所有可能出现的结果,并写出恰好配成形同颜色的一双拖鞋的概率.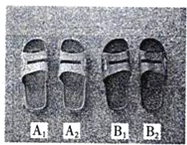
如图,有两个边长为2的正方形,将其中一个正方形沿对角线剪开成两个全等的等腰直角三角形,用这三个图片分别在网格备用图的基础上(只要再补出两个等腰直角三角形即可),分别拼出一个三角形、一个四边形、一个五边形、一个六边形.