如图a所示,用铁架台、弹簧和多个已知质量且质量相等的钩码,探究在弹性限度内弹簧弹力与弹簧伸长量的关系.
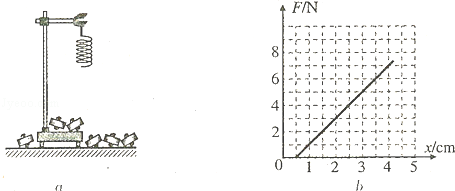
①为完成实验,还需要的实验器材有: .
②图b是弹簧所受弹力F与弹簧伸长量x的关系图线,由此可求出弹簧的劲度系数为 N/m.图线不过原点的原因是由于 .
在“验证机械能守恒定律”的实验中,质量为1kg的重锤自由下落,通过打点计时器在纸带上记录运动过程,打点计时器所接电源频率为50Hz。如图所示,纸带上O点为重锤自由下落时纸带打点起点,选取的计数点A、B、C、D依次间隔一个点(图中未画出),各计数点与O点距离如图所示,单位为mm,重力加速度为9.80 m/s2 ,则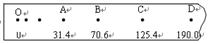
(1)打点计时器记录B点时,重锤速度vB=______ _ m/s,重锤动能EKB=__________J.
_ m/s,重锤动能EKB=__________J.
(2)从开始下落算起,打点计时器记录B点时,重锤势能减少量为J.
(19分)(1)为了测定一节干电池的电动势和内电阻,某实验小组按图甲所示的电路连好实验电路图,合上开关,电流表和电压表的读数正常,当将滑动变阻器的滑动触头由A端向B端逐渐滑动时,发现电流表的示数逐渐增大,而电压表的示数接近1.5V且几乎不变,直到当滑动触头滑至临近B端时电压表的示数急剧变化,这种情况很难读出电压数值分布均匀的几组不同的电流、电压值,出现上述情况的原因是_________________;改进的办法是_________________________;改进后,测出几组电流、电压的数值,并画出图像如图乙所示,由图像可知,这个电池的电动势E = ____________V,内电阻r = ____________ .
.

(2)某同学和你一起探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k.做法是先将待测弹簧的一端固定在铁架台上,然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上.当弹簧自然下垂时,指针指示的刻度数值记作L0,弹簧下端挂一个50g的砝码时,指针指示的刻度数值记作L1;弹簧下端挂两个50g的砝码时,指针指示的刻度数值记作L2;……;挂七个50g的砝码时,指针指示的刻度数值记作L7.
①下表记录的是该同学已测出的6个值,其中有两个数值在记录时有误,它们的代表符号分别是和.
测量记录表:
| 代表符号 |
L0 |
L1 |
L2 |
L3 |
L4 |
L5 |
L6 |
L7 |
| 刻度数值/cm |
1.70 |
3.40 |
5.10 |
6.85 |
8.60 |
10.3 |
12.1 |
13.95 |
②为充分利用测量数据,该同学将所测得的数值按如下方法逐一求差,分别计算出了三个差值: cm,
cm, cm,
cm, cm
cm
请你给出第四个差值:d4 ==cm.
③根据以上差值,可以求出每增加50g砝码的弹簧平均伸长量△L.△L用d1、d2、d3、d4表示的式子为:△L=,代入数据解得△L=cm.
④计算弹簧的劲度系数k=N/m.(g取9.8 m/s2,此空保留两位有效数字)
实验装置如图1所示;一木块放在水平长木板上,左侧拴有一细软线,跨过固定在木板边缘的滑轮与一重物相连,木块右侧与打点计时器的纸带相连,在重物牵引下,木块在木板上向左运动,重物落地后,木块继续向左做匀减速运动,图2给出了重物落地后,打点计时器在纸带上打出的一些点,试根据给出的数据,求木块与木板间的摩擦因数μ。要求写出主要的运算过程,结果保留2位有效数字。(打点计时器所用交流电频率为50Hz,不计纸带与木块间的拉力。取重力加速度g=10m/s2)

(1)以下是“探究弹力和弹簧伸长的关系”的实验步骤,按操作的先后顺序排列起来是
| A.以弹簧伸长长度x 为横坐标,以弹力F为纵坐标,描出各组数据(x,F)对应的点,并用平滑的曲线将点连结起来 |
| B.记下弹簧不挂钩码时,其下端在刻度尺上的刻度L0 |
| C.将铁架台置于水平桌面上,并将弹簧的一端系于横梁上,在弹簧附近竖直固定一刻度尺 |
| D.依次在弹簧的下端挂上1个、2个、3个、4个…钩码,并分别记下钩码静止时,弹簧下端所对应的刻度尺上的刻度并记录在表格内,然后取下钩码 |
E.写出弹力随弹簧伸长量之间的变化关系
F.解释函数表达式中常数的物理意义
(2)发光晶体二极管是用电器上做指示灯用的一种电子元件.它的电路符号如图甲所示,正常使用时,带“+”号的一端接高电势,带“-”的一端接低电势.某同学用实验方法探究二极管的伏安特性曲线,现测得它两端的电压U和通过它的电流 I的数据如表中所示.
| U / V |
0 |
0.4 |
0.8 |
1.2 |
1.6 |
2.0 |
2.4 |
2.6 |
2.8 |
3.0 |
| I / mA |
0 |
0.9 |
2.3 |
4.3 |
6.8 |
13.0 |
19.0 |
24.0 |
30.0 |
37.0 |
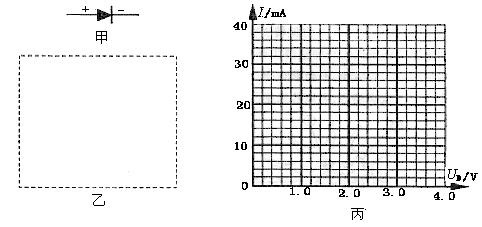
①在图乙中的虚线框内画出实验电路图.(除电源、开关、滑动变阻器外;实验用电压表V:内组RV 约为10kΩ,电流表mA:内阻 RA约为100Ω)
②在图(丙)中的小方格纸上用描点法画出二极管的伏安特性曲线.
③根据②中画出的二极管的伏安特性曲线,简要说明发光二极管的电阻与其两端电压的关系:.
下图是某实验小组同学利用打点计时器,测量某物块做匀变速直线运动时得到的一条纸带,取O点为t=0时刻记时点,各连续点间的时间间隔为0.02s。
(1)图中a、c、e三点的计数是
xa=、xc=、xe=。
(2)说明该物体运动的方向与受合外力方向的关系。
(3)用a、c、e三点的数据,计算出物体运动的加速度(要求写出计算过程)。