光滑水平桌面上方存在垂直桌面向上范围足够大的匀强磁场,虚线框abcd内存在平行于桌面的匀强电场,如图所示,一带电小球从d处静止开始运动到b处时的速度方向与电场边界平行,通过磁场作用又回到d点,已知bc=2ab=2L,磁感应强度为B,小球的质量为m,电荷量为q,试分析求解
(1)小球的带电性质从d到b的运动性质
(2)小球子磁场中运动速度大小
(3)在电场中达到b位置的曲率半径
如图所示,在空间内有一直角坐标系 ,直线
,直线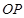 与
与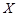 轴正方向夹角为
轴正方向夹角为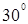 。第一象限内有两个方向均垂直纸面向外的匀强磁场区域Ⅰ和Ⅱ,直线
。第一象限内有两个方向均垂直纸面向外的匀强磁场区域Ⅰ和Ⅱ,直线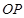 是它们的理想边界,
是它们的理想边界,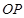 上方区域Ⅰ中磁场的磁感应强度为
上方区域Ⅰ中磁场的磁感应强度为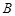 ,在第四象限内有一沿
,在第四象限内有一沿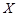 轴负方向的匀强电场。一质量为
轴负方向的匀强电场。一质量为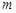 、电荷量为
、电荷量为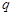 的质子(不计重力及质子对磁场、电场的影响)以速度
的质子(不计重力及质子对磁场、电场的影响)以速度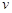 从
从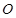 点沿与
点沿与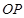 成
成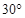 角方向垂直磁场进入区域Ⅰ,质子先后通过磁场区域Ⅰ和Ⅱ后,恰好垂直通过
角方向垂直磁场进入区域Ⅰ,质子先后通过磁场区域Ⅰ和Ⅱ后,恰好垂直通过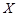 轴上的
轴上的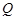 点(未画出)进入第四象限内的匀强电场中,最后从
点(未画出)进入第四象限内的匀强电场中,最后从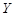 轴上的
轴上的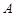 点与
点与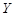 轴负方向成
轴负方向成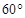 角射出,求:
角射出,求: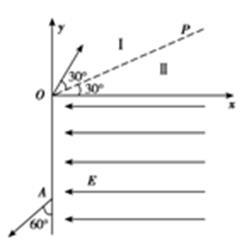
(1)区域Ⅱ中磁场的磁感应强度大小;
(2)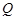 点到
点到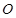 点的距离;
点的距离;
(3)匀强电场的电场强度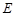 的大小
的大小
用如图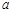 所示的水平——斜面装置研究平抛运动,一物块(可视为质点)置于粗糙水平面上的O点,O点距离斜面顶端P点为S。每次用水平拉力F,将物块由O点从静止开始拉动,当物块运动到P点时撤去拉力F。实验时获得物块在不同拉力作用下落在斜面上的不同水平射程
所示的水平——斜面装置研究平抛运动,一物块(可视为质点)置于粗糙水平面上的O点,O点距离斜面顶端P点为S。每次用水平拉力F,将物块由O点从静止开始拉动,当物块运动到P点时撤去拉力F。实验时获得物块在不同拉力作用下落在斜面上的不同水平射程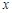 ,做出了如图
,做出了如图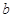 所示的
所示的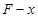 图像,若水平面上的动摩擦因数为
图像,若水平面上的动摩擦因数为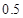 ,斜面与水平地面之间的夹角
,斜面与水平地面之间的夹角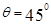 ,
,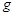 取
取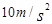 ,设最大静摩擦力等于滑动摩擦力。求:
,设最大静摩擦力等于滑动摩擦力。求: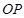 间的距离S是多少?(保留两位有效数字)
间的距离S是多少?(保留两位有效数字)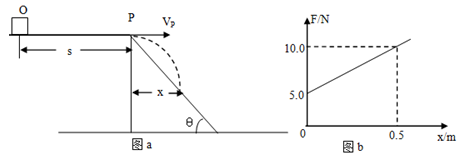
如图所示,x轴与水平传送带重合,坐标原点0在传送带的左端,传送带OQ长 L=8m,传送带顺时针速度 =5m/s,—质量m=1kg的小物块轻轻放在传送带上xp=2m的P点,小物块随传送带运动到Q点后恰好能冲上光滑圆弧轨道的最高点N点。小物块与传送带间的动摩擦因数μ=0.5,重力加速度g=10m/s2,求:
=5m/s,—质量m=1kg的小物块轻轻放在传送带上xp=2m的P点,小物块随传送带运动到Q点后恰好能冲上光滑圆弧轨道的最高点N点。小物块与传送带间的动摩擦因数μ=0.5,重力加速度g=10m/s2,求: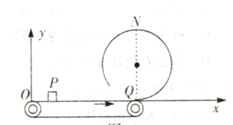
(1)N点的纵坐标;
(2)若将小物块轻放在传送带上的某些位置,小物块均能沿光滑圆弧轨道运动(小物块始终在圆弧轨道运动不脱轨)到达纵坐标yM=0.25m的M点,求这些位置的横坐标范围。
如图甲所示,有一倾角为30°的光滑固定斜面,斜面底端的水平面上放一质量为M的木板.开始时质量为m=1kg的滑块在水平向左的力F作用下静止在斜面上,今将水平力F变为水平向右,当滑块滑到木板上时撤去力F,木块滑上木板的过程不考虑能量损失.此后滑块和木板在水平上运动的v﹣t图象如图乙所示,g=10m/s2.求
(1)水平作用力F的大小;
(2)滑块开始下滑时的高度;
(3)木板的质量.
未来“嫦娥五号”落月后,轨道飞行器将作为中继卫星在绕月轨道上做圆周运动,如图所示.设卫星距离月球表面高为h,绕行周期为T,已知月球绕地球公转的周期为T0,地球半径为R,地球表面的重力加速度为g,月球半径为r,万有引力常量为G.试分别求出: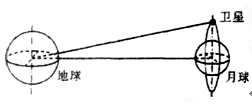
(1)地球的质量和月球的质量;
(2)中继卫星向地球发送的信号到达地球,最少需要多长时间?(已知光速为c,且h≤r≤R)